cho nửa đường tròn tam o đường kính cd= 2r từ điểm c vẽ tiếp tuyến cx của nửa đường tròn, lấy điểm m thuộc nửa đường tròn. kẻ tia dm cắt cx tại e ( e là giao điểm) kẻ mh vuông góc cd tại h....
chứng minh
a) tam giác dcm là tam giác gì vì sao
b) Md.ED=4r2
c) ch.cd = me.md
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
12 tháng 12 2019
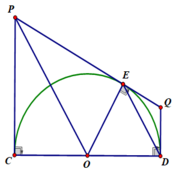
Xét tứ giác CPEO có:
∠(PCO) = ∠(PEO) = 90 0 (gt)
⇒ ∠(PCO) + ∠(PEO) = 180 0
⇒ Tứ giác CPEO là tứ giác nội tiếp
Xét tứ giác OEQD có:
∠(OEQ) = ∠(ODQ) = 90 0 (gt)
⇒ ∠(OEQ) + ∠(ODQ) = 180 0
⇒ Tứ giác OEQD là tứ giác nội tiếp

1 tháng 4 2023
góc CID=1/2*180=90 độ
=>CI vuông góc HD
góc CND=1/2*180=90 độ
=>DN vuông góc CH
Vì góc HNM+góc HIM=180 độ
nên HNMI nội tiếp
Xét ΔGCD vuông tại C có CN là đường cao
nên CN^2=NG*ND
⇒ ∆DCM vuông tại M
b) Do CE là tiếp tuyến tại C của nửa đường tròn
⇒ CE ⊥ CD
⇒ ∆CDE vuông tại C
Do ∆DCM vuông tại M (cmt)
⇒ CM ⊥ CD
⇒ CM ⊥ DE
⇒ CM là đường cao của ∆CDE
Do ∆CDE vuông tại C, có CM là đường cao
⇒ CD² = MD.ED
⇒ MD.ED = (2r)²
⇒ MD.ED = 4r²
c) ∆DCM vuông tại M, có MH là đường cao
⇒ CH.CD = CM² (1)
∆CDE vuông tại C, có CM là đường cao
⇒ ME.MD = CM² (2)
Từ (1) và (2) ⇒ CH.CD = ME.MD