Viết khai triển (2x-3y)^10 bằng nhị thức Newton
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(A_n^2 + 24C_n^1 = \frac{{n!}}{{\left( {n - 2} \right)!}} + 24.\frac{{n!}}{{1!\left( {n - 1} \right)!}} = n(n - 1) + 24n\)
\( \Leftrightarrow {n^2} + 23n = 140 \Leftrightarrow \left[ \begin{array}{l}n = 5\\n = - 28\;(L)\end{array} \right.\)
Thay \(a = 2x,b = - 1\) trong công thức khai triển của \({(a + b)^5}\), ta được:
\(\begin{array}{l}{(2x - 1)^5} = {\left( {2x} \right)^5} + 5.{\left( {2x} \right)^4}.( - 1) + 10.{\left( {2x} \right)^3}.{( - 1)^2}\\ + 10.{\left( {2x} \right)^2}.{( - 1)^3} + 5.(2x).{( - 1)^4} + {( - 1)^5}\\ = 32{x^5} - 80{x^4} + 80{x^3} - 40{x^2} + 10x - 1\end{array}\)

Ta có:
\({(2x + 3)^5} = 32{x^5} + 240{x^4} + 720{x^3} + 1080{x^2} + 810x + 243\)
Hệ số của \({x^3}\) là 720
Hệ số của \({x^4}\) là 240.
Vậy hệ số của \({x^3}\) lớn hơn hệ số của \({x^4}\).

Đáp án C
2 − x n = ∑ k = 0 n C n k − x k .2 n − k ⇒ hệ số của x 4 là: C n 4 − 1 4 .2 n − 4 = 280 ⇔ n = 7
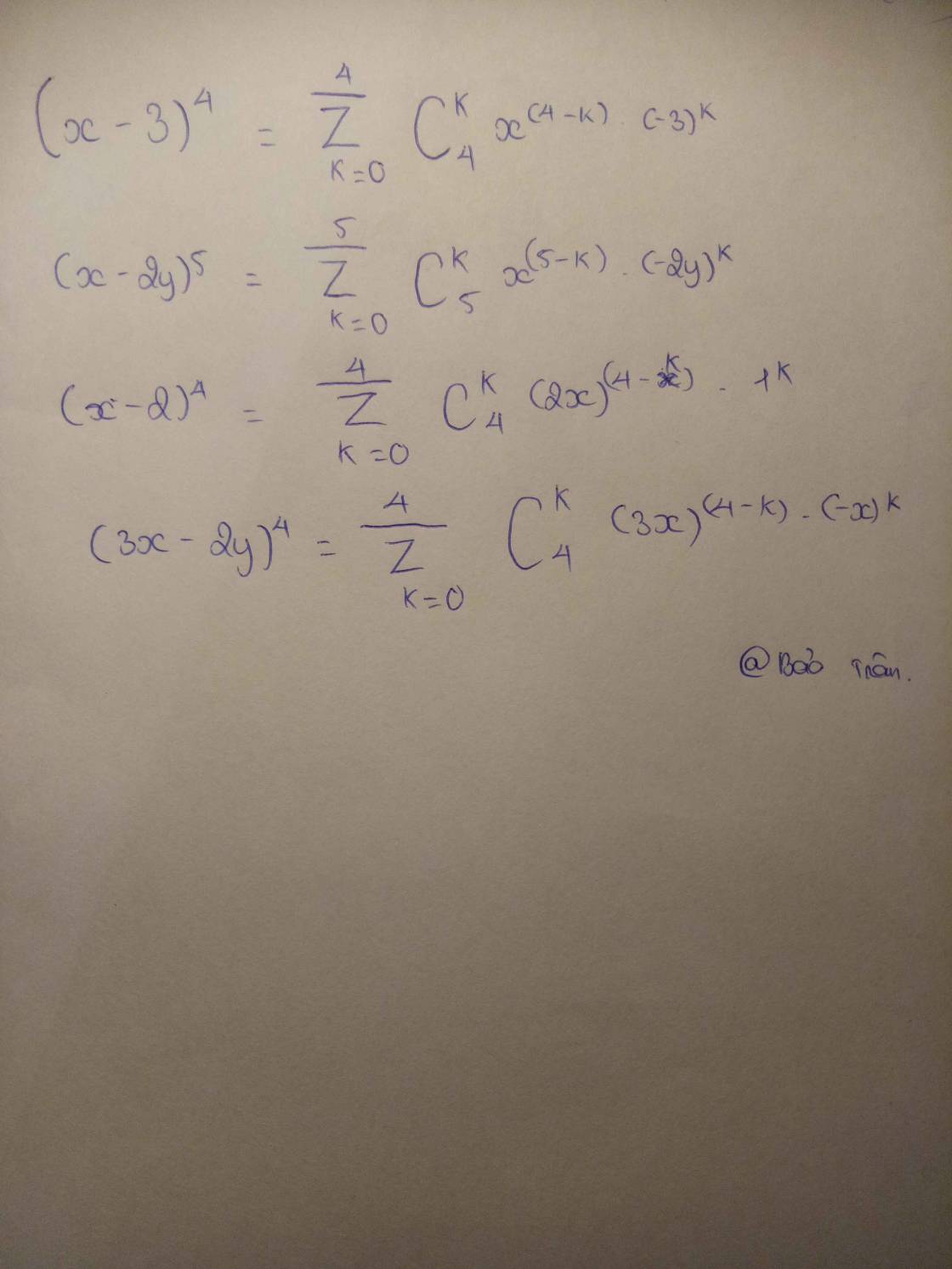


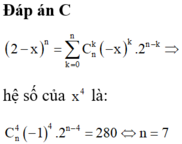
\(\left(2x-3y\right)^{10}\)
\(=\left(2x\right)^{10}-C^1_{10}\cdot\left(2x\right)^9\cdot3y+C^2_{10}\cdot\left(2x\right)^8\cdot\left(3y\right)^2+...+\left(3y\right)^{10}\)
\(=1024x^{10}-1536x^9y+...+59049y^{10}\)