Cho tam giác ABC, góc B= 60o, C=40o. Phân giác của góc BAD cắt BC ở D. Kẻ AH vuông góc với BC tại H. Tính HAD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có:
Góc A + góc B + góc C = 180o
=> Góc C = 180o - ( góc A + góc B)
=> Góc C = 180o - ( 90o + 60o)
=> Góc C = 30o
b, Vì AD là tia phân giác góc A
Mà góc A = 90o (giả thiết)
=> Góc BAD = DAC = 90o : 2 = 45o
Ta có: Góc BAD + góc ABD + góc ADB = 180o
=> 45o + 60o + góc ADB = 180o
=> góc ADB = 75o
c, Ta có: góc AHD + góc HDA + góc DAH = 180o
=> góc DAH = 180o - 90o - 75o
=> góc DAH = 15o

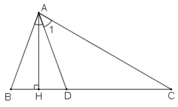
ΔADH vuông tại H nên:
∠(HAD) + ∠(ADH) = 90o (tính chất tam giác vuông)
⇒∠ (HAD) = 90o-∠(ADH)o = 90o - 70o = 20o

a: Xét ΔADC có
\(\widehat{ADC}+\widehat{DAC}+\widehat{C}=180^0\)
\(\Leftrightarrow\widehat{ADH}=180^0-30^0-45^0\)
hay \(\widehat{ADH}=105^0\)