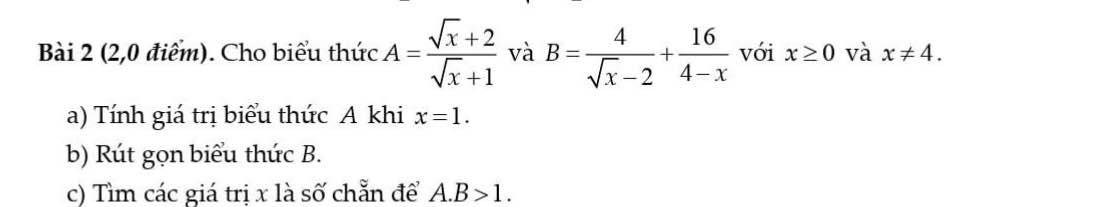 Làm e câu c thoi a
Làm e câu c thoi a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Các vị trí so le trong, và đồng vị với \(\widehat{mAB}\) là:
\(\widehat{B_1};\widehat{APQ};\widehat{nPA}\)
b) Ta có: \(\widehat{B_1}=\widehat{mAB}=50^o\) (hai góc so le trong)
Mà: \(\widehat{B_1}+\widehat{B_2}=180^o\Rightarrow\widehat{B_2}=180^o-50^o=130^o\)
c) Ta có: \(\widehat{mAB}+\widehat{A_1}=180^o\Rightarrow\widehat{A_1}=180^o-\widehat{mAB}=180^o-50^o=130^o\)
Mà: \(\widehat{mAB}=\widehat{A_2}=50^o\)(hai góc đối đỉnh)
d) Ta có:
\(\widehat{APQ}+\widehat{PQB}=180^o\)
\(\Rightarrow\widehat{PQB}=180^o-\widehat{APQ}=180^o-110^o=70^o\)

Bài 4:
a: Xét tứ giác ABEC có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AE
Do đó: ABEC là hình bình hành
mà AB=AC
nên ABEC là hình thoi
b: Ta có: ABEC là hình thoi
nên \(\widehat{BAC}=\widehat{BEC}\)
hay \(\widehat{BEC}=60^0\)

a) 7/5 : 3/2 = 14/15
b) 3/4 : 2/5 : 3/7
= 15/8 : 3/7
= 35/8
c) 9/2 : 1/2 - 7/4
= 9 - 7/4
= 29/4

a: Xét tứ giác AEGK có
GK//AE
GK=AE
Do đó: AEGK là hình bình hành
mà \(\widehat{KAE}=90^0\)
nên AEGK là hình chữ nhật

Lời giải:
a. $(a+b-c)-(b-c+d)=a+b-c-b+c-d=a+(b-b)+(-c+c)-d=a+0+0-d=a-d$
b. $(a-b+d)-(a-b+c)=a-b+d-a+b-c=(a-a)+(-b+b)+(d-c)=0+0+d-c=d-c$
c. $(a+b)-(b-c-a)=a+b-b+c+a=(a+a)+(b-b)+c=2a+0+c=2a+c$
d. $-(a-b)+(a-b+c)=-a+b+a-b+c=(-a+a)+(b-b)+c=0+0+c=c$
e. $(a-b+c)-(a-b+c)=a-b+c-a+b-c=(a-a)+(-b+b)+(c-c)=0+0+0=0$
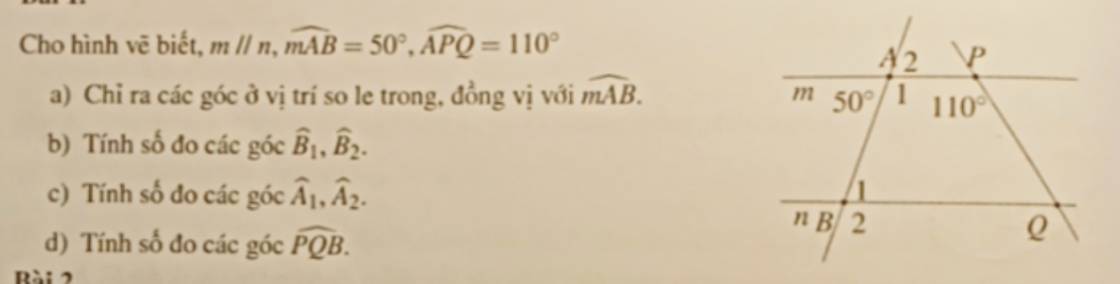
a: Khi x=1 thì \(A=\dfrac{1+2}{1+1}=\dfrac{3}{2}\)
b: \(B=\dfrac{4}{\sqrt{x}-2}+\dfrac{16}{4-x}\)
\(=\dfrac{4}{\sqrt{x}-2}-\dfrac{16}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{4\left(\sqrt{x}+2\right)-16}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{4\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{4\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{4}{\sqrt{x}+2}\)
c: Đặt P=A*B
\(=\dfrac{4}{\sqrt{x}+2}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}=\dfrac{4}{\sqrt{x}+1}\)
Để P>1 thì P-1>0
=>\(\dfrac{4}{\sqrt{x}+1}-1>0\)
=>\(\dfrac{4-\sqrt{x}-1}{\sqrt{x}+1}>0\)
=>\(3-\sqrt{x}>0\)
=>\(\sqrt{x}< 3\)
=>0<=x<9
mà x chẵn và x<>4
nên \(x\in\left\{0;2;6;8\right\}\)