Cho điểm B(-1,3) và đường thẳng (d) :x+y-2=0. a) viết ptđt có tâm I(3;6) và đi qua điểm B. b)Viết ptđt đenta vuông góc với đường thẳng d và cắt 2 trúc tọa độ tại 2 điểm M,N sao cho diện tích tam giác BMN =5/2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Trục Ox có pt \(y=0\) nên đường song song với nó là \(y=4\)
2.
\(\overrightarrow{MI}=\left(1;-2\right)\)
Đường thẳng tiếp xúc với đường tròn tâm I tại M đi qua M và vuông góc MI nên nhận \(\overrightarrow{MI}\) là 1 vtpt
Phương trình:
\(1\left(x-1\right)-2\left(y-3\right)=0\Leftrightarrow x-2y+5=0\)

`a)` Gọi đường thẳng `\Delta` song song với `d` là: `3x+4y+c=0` `(c ne 5)`
Mà `I in \Delta`
`=>2.1+4.3+c=0<=>c=-14` (t/m)
`=>PTTQ` của `\Delta` là: `3x+4y-14=0`
`b)` Có: `R=d(I;d)=[|3.1+4.3+5|]/[\sqrt{3^2+4^2}]=4`
`=>` Ptr đường tròn tâm `I` bán kinh `R=4` là:
`(x-1)^2+(y-3)^2=16`

gọi H là trung điểm AB
=>IH⊥AB
=>\(d_{\left(I,d\right)}=\dfrac{\left|1\cdot1-1\cdot1+2\right|}{\sqrt{1^2+\left(-1\right)^2}}=\sqrt{2}\)
=>IH=\(\sqrt{2}\)
Mà HB=\(\dfrac{AB}{2}\)=1
Xét ΔIHB vuông tại H có:
IB=\(\sqrt{IH^2+HB^2}=\sqrt{2+1}=\sqrt{3}\)
=>R=\(\sqrt{3}\)
Vậy đường tròn tâm I (1; -1); R=\(\sqrt{3}\) là:
(x-1)2+(y+1)2=3

REFER
https://hoc24.vn/index.php/cau-hoi/trong-mat-phang-oxy-cho-diem-i-1-1-va-duong-thang-d-xy20-viet-phuong-trinh-duong-tron-tam-i-cat-d-tai-hai-diem-ab-sao-cho-ab2.5543217878093

\(d\left(I;d\right)=\dfrac{\left|-1+1+2\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Gọi H là trung điểm AB \(\Rightarrow IH\perp AB\Rightarrow IH=d\left(I;d\right)=\sqrt{2}\)
Áp dụng định lý Pitago:
\(R^2=IA^2=IH^2+AH^2=IH^2+\left(\dfrac{AB}{2}\right)^2=3\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-1\right)^2=3\)

1.
\(cos\alpha=-\sqrt{1-sin^2\alpha}=-\dfrac{4}{5}\)
\(\Rightarrow sin\left(\alpha+\dfrac{\pi}{3}\right)=sin\alpha.cos\dfrac{\pi}{3}+cos\alpha.sin\dfrac{\pi}{3}\)
\(=-\dfrac{3}{5}.\dfrac{1}{2}-\dfrac{4}{5}.\dfrac{\sqrt{3}}{2}\)
\(=-\dfrac{15+8\sqrt{3}}{20}\)

a) Phương trình đường tròn \(\left( C \right)\) là: \({\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 49\).
b) Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( { - 2 - 1} \right)}^2} + {{\left( {2 - \left( { - 2} \right)} \right)}^2}} = 5\)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 25\)
c) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( { - 2;1} \right)\)
Bán kính đường tròn là: \[R = IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( { - 3 - 1} \right)}^2}} = \sqrt {17} \]
Phương trình đường tròn là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 17\)
d) Bán kính đường tròn là: \(R = \frac{{\left| {1 + 2.3 + 3} \right|}}{{\sqrt {{1^2} + {2^2}} }} = 2\sqrt 5 \)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 20\)
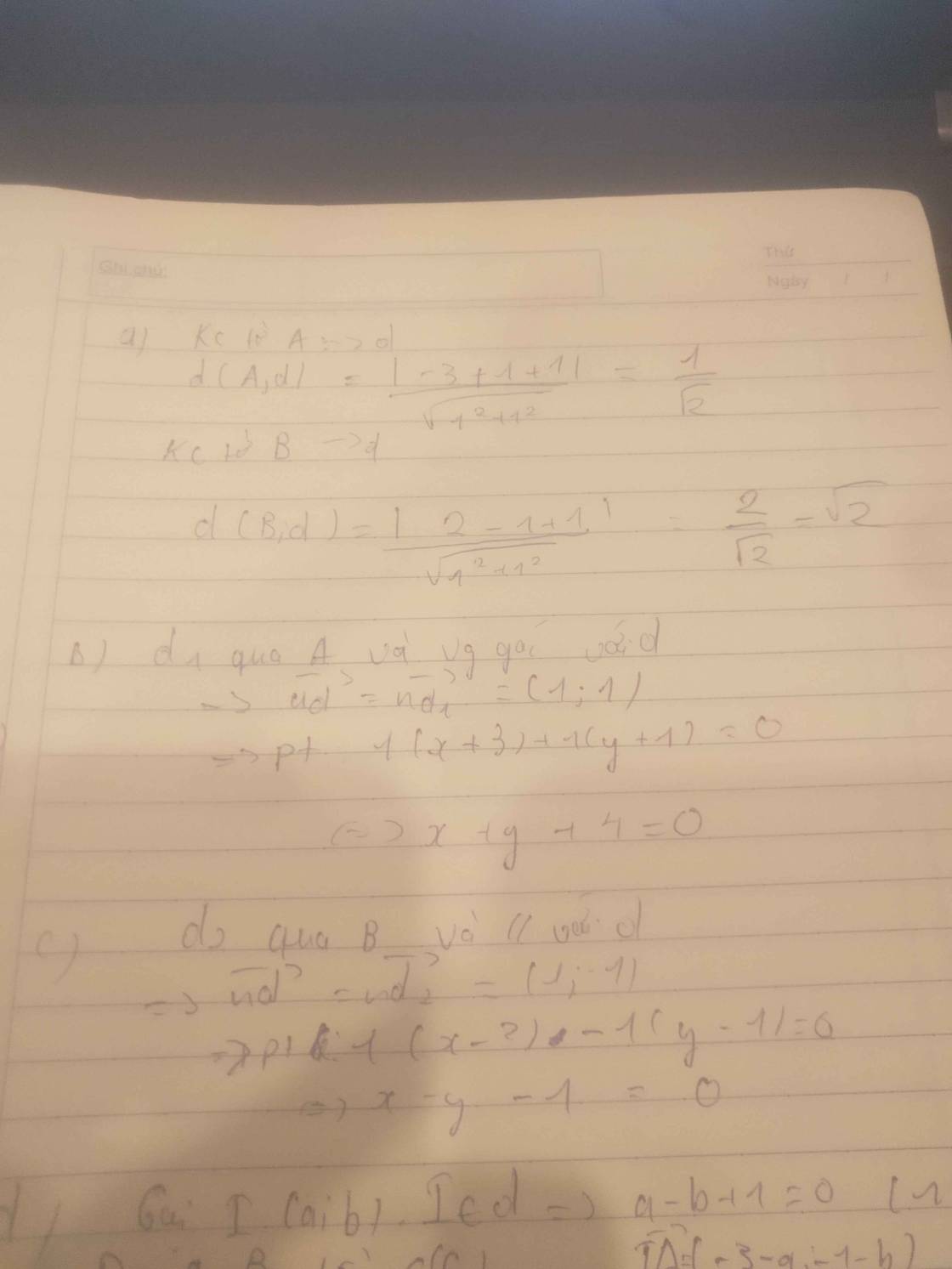
a. \(\overrightarrow{BI}=\left(4;3\right)\Rightarrow R^2=IB^2=4^2+3^2=25\)
Phương trình đường tròn:
\(\left(x-3\right)^2+\left(y-6\right)^2=25\)
b.
\(\Delta\) vuông góc d nên nhận (1;-1) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(x-y+c=0\)
Giả sử M là giao điểm \(\Delta\) với Ox và N là giao điểm với Oy \(\Rightarrow M\left(-c;0\right)\) ; \(N\left(0;c\right)\)
\(\Rightarrow\overrightarrow{MN}=\left(c;c\right)\Rightarrow MN=\sqrt{c^2+c^2}=\left|c\right|\sqrt{2}\)
\(S_{BMN}=\dfrac{1}{2}MN.d\left(B;MN\right)=\dfrac{1}{2}.\left|c\right|\sqrt{2}.\dfrac{\left|-1-3+c\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{5}{2}\)
\(\Rightarrow\left|c^2-4c\right|=5\Rightarrow\left[{}\begin{matrix}c^2-4c=5\\c^2-4c=-5\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}c=-1\\c=5\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}x-y-1=0\\x-y+5=0\end{matrix}\right.\)