cho tam giác ABC có A = 90o
Kẻ AH\(⊥BC\) ( H \(\in BC\))
Các tia phân giác của các góc BAH và C cắt nhau tại K
Chứng minh : AC \(⊥\)CK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 8 2017
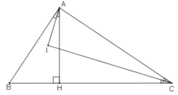
Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H
Trong tam giác vuông AHB ta có: ∠BHA = 90o
⇒ ∠B + ∠BAH = 90o (1)
Trong tam giác vuông ABC ta có: ∠BAC = 90o
⇒ ∠B + ∠C = 90o (2)
Từ (1) và (2) suy ra: ∠BAH = ∠C (3)
+) Vì AI là tia phân giác của góc BAC nên:
∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)
Do CI là tia phân giác của góc ACB nên:
∠(ACI) = ∠(ICB) = 1/2.∠C (5)
+) Từ (3); (4) và (5) suy ra:
∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)
+) Lại có:
∠BAI + ∠IAC = 90º
Suy ra: ∠ICA + ∠IAC = 90º
Trong ΔAIC có: ∠ICA+ ∠IAC = 90º
Vậy: ∠AIC = 90º.
29 tháng 12 2019
Ta có : \(\Delta AHC\) có \(\widehat{H}=90^o\) nên \(\widehat{ACH}+\widehat{A_3}=90^o\) (1)
Ta lại có :
\(\widehat{BAH}+\widehat{A_3}=\widehat{BAC}=90^o\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{ACH}=\widehat{BAH}\)
Ta có :
\(\widehat{C_1}=\frac{1}{2}\widehat{ACH}\)nên \(\widehat{C}_1=\widehat{A_1}\)
Do đó \(\widehat{A_2}+\widehat{A_3}+\widehat{C}_1=\widehat{A}_2+\widehat{A}_3+\widehat{A}_1=90^o\)
Tam giác AKC có : \(\widehat{A}_2+\widehat{A_3}+\widehat{C}_1=90^o\) . Vậy \(AK\perp CK\)
Chúc bạn học tốt !!!