gúip mik mấy bài vs
gúip mik mấy bài vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 7:
a)ĐKXĐ:\(\left\{{}\begin{matrix}x\ge m+1\\x\ge\dfrac{m}{4}\end{matrix}\right.\)
TH1: \(m+1< \dfrac{m}{4}\Rightarrow m< -\dfrac{4}{3}\)
\(\Rightarrow x\ge\dfrac{m}{4}\)\(\Rightarrow x\in\)\([\dfrac{m}{4};+\)\(\infty\)\()\)
Để hàm số xác định với mọi x dương \(\Leftrightarrow\)\(\left(0;+\infty\right)\subset\)\([\dfrac{m}{4};+\)\(\infty\)\()\)
\(\Leftrightarrow\dfrac{m}{4}\ge0\Leftrightarrow m\ge0\) kết hợp với \(m< -\dfrac{4}{3}\Rightarrow m\in\varnothing\)
TH2:\(m+1\ge\dfrac{m}{4}\Rightarrow m\ge-\dfrac{4}{3}\)
\(\Rightarrow x\ge m+1\)\(\Rightarrow\)\(x\in\)\([m+1;+\)\(\infty\))
Để hàm số xác định với mọi x dương \(\Leftrightarrow\)\(\left(0;+\infty\right)\subset\)\([m+1;\)\(+\infty\)\()\)
\(\Leftrightarrow m+1\le0\Leftrightarrow m\le-1\) kết hợp với \(m\ge-\dfrac{4}{3}\)
\(\Rightarrow m\in\left[-\dfrac{4}{3};-1\right]\)
Vậy...
b)ĐKXĐ:\(\left\{{}\begin{matrix}x\ge2-m\\x\ne-m\end{matrix}\right.\)\(\Rightarrow x\in\)\([2-m;+\)\(\infty\)) (vì \(-m< 2-m\))
Để hàm số xác ddingj với mọi x dương
\(\Leftrightarrow\left(0;+\infty\right)\subset\)\([2-m;+\)\(\infty\))
\(\Leftrightarrow2-m\le0\Leftrightarrow m\ge2\)
Vậy...
Bài 9:
a)Đặt \(f\left(x\right)=x^2+2x-2\)
TXĐ:\(D=R\)
TH1:\(x\in\left(-\infty;-1\right)\)
Lấy \(x_1;x_2\in\left(-\infty;-1\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-\left(x_2^2+2x_2-2\right)}{x_1-x_2}=x_1+x_2+2\)
Vì \(x_1;x_2\in\left(-\infty;-1\right)\Rightarrow x_1+x_2< -1+-1=-2\)\(\Leftrightarrow x_1+x_2+2< 0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(-\infty;-1\right)\)
TH2:\(x\in\left(-1;+\infty\right)\)
Lấy \(x_1;x_2\in\left(-1;+\infty\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-\left(x_2^2+2x_2-2\right)}{x_1-x_2}=x_1+x_2+2>0\)
Suy ra hàm đb trên \(\left(-1;+\infty\right)\)
Vậy...
b)Đặt \(f\left(x\right)=\dfrac{2}{x-3}\)
TXĐ:\(D=R\backslash\left\{3\right\}\)
TH1:\(x\in\left(-\infty;3\right)\)
Lấy \(x_1;x_2\in\left(-\infty;3\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{2}{x_1-3}-\dfrac{2}{x_2-3}}{x_1-x_2}=\dfrac{-2}{\left(x_1-3\right)\left(x_2-3\right)}\)
Vì \(x_1;x_2\in\left(-\infty;3\right)\Rightarrow x_1-3< 0;x_2-3< 0\Rightarrow\left(x_1-3\right)\left(x_2-3\right)>0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(-\infty;3\right)\)
TH2:\(x\in\left(3;+\infty\right)\)
Lấy \(x_1;x_2\in\left(3;+\infty\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{2}{x_1-3}-\dfrac{2}{x_2-3}}{x_1-x_2}=\dfrac{-2}{\left(x_1-3\right)\left(x_2-3\right)}\)
Vì \(x_1;x_2\in\left(3;+\infty\right)\Rightarrow x_1-3>0;x_2-3>0\Rightarrow\left(x_1-3\right)\left(x_2-3\right)>0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(3;+\infty\right)\)
Vậy hàm nb trên \(\left(-\infty;3\right)\) và \(\left(3;+\infty\right)\)

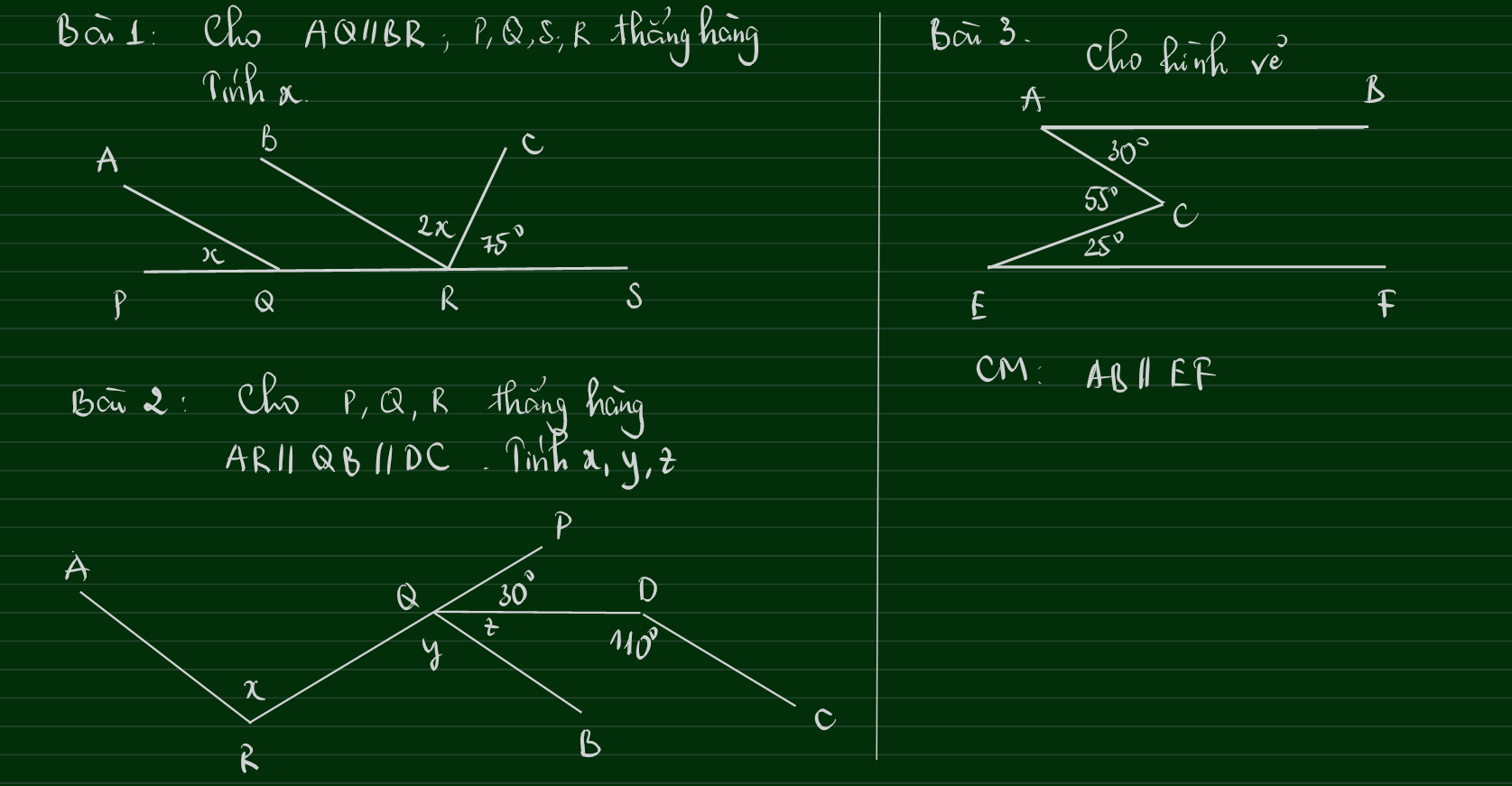
Bài 1:
Vì $AQ\parallel BR$ nên $\widehat{PQA}=\widehat{QRB}$ (hai góc đồng vị )
$\Rightarrow \widehat{QRB}=x$
Lại có:
$Q,R,S$ thẳng hàng nên
$\widehat{QRS}=180^0$
$\widehat{QRB}+\widehat{BRC}+\widehat{CRS}=180^0$
$x+2x+75^0=180^0$
$3x+75^0=180^0$
$x=35^0$

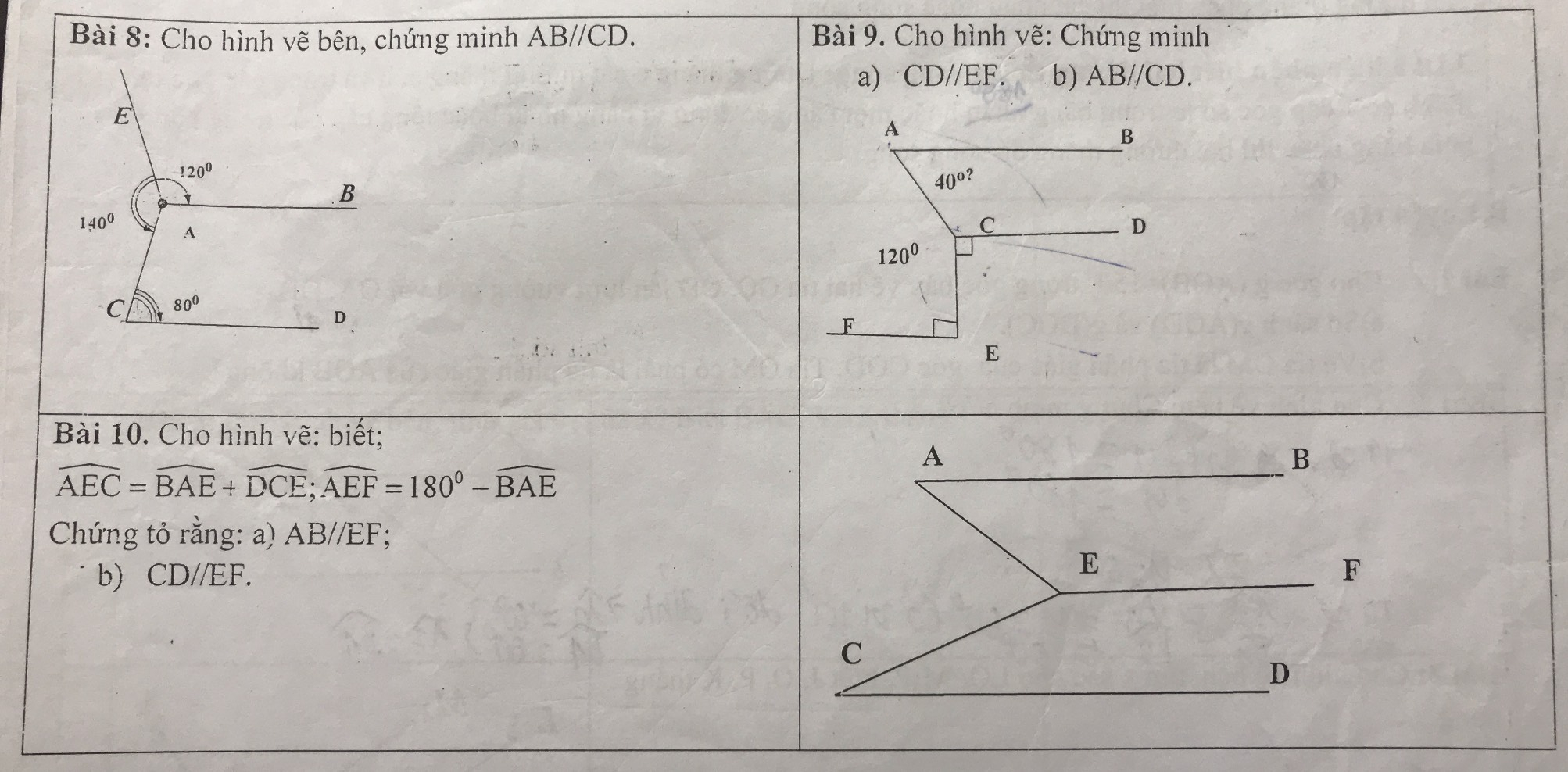

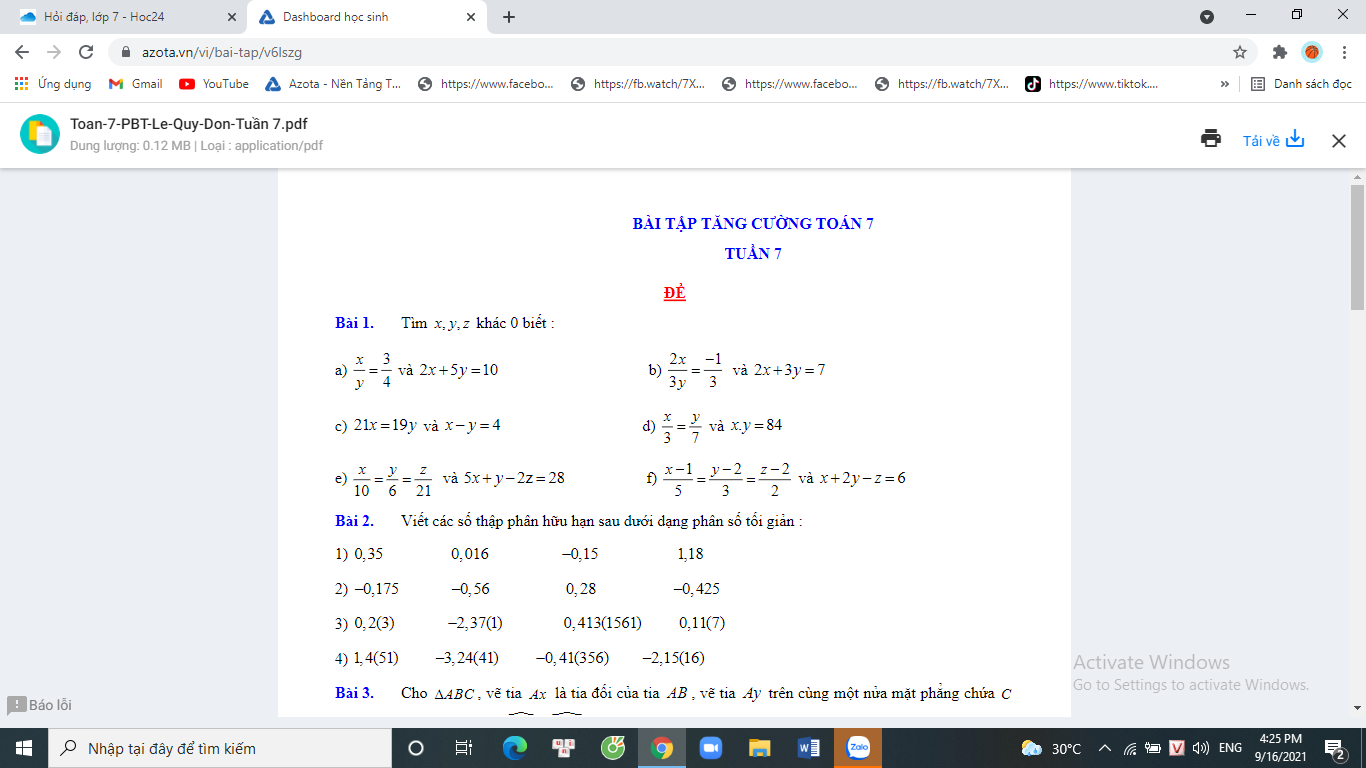
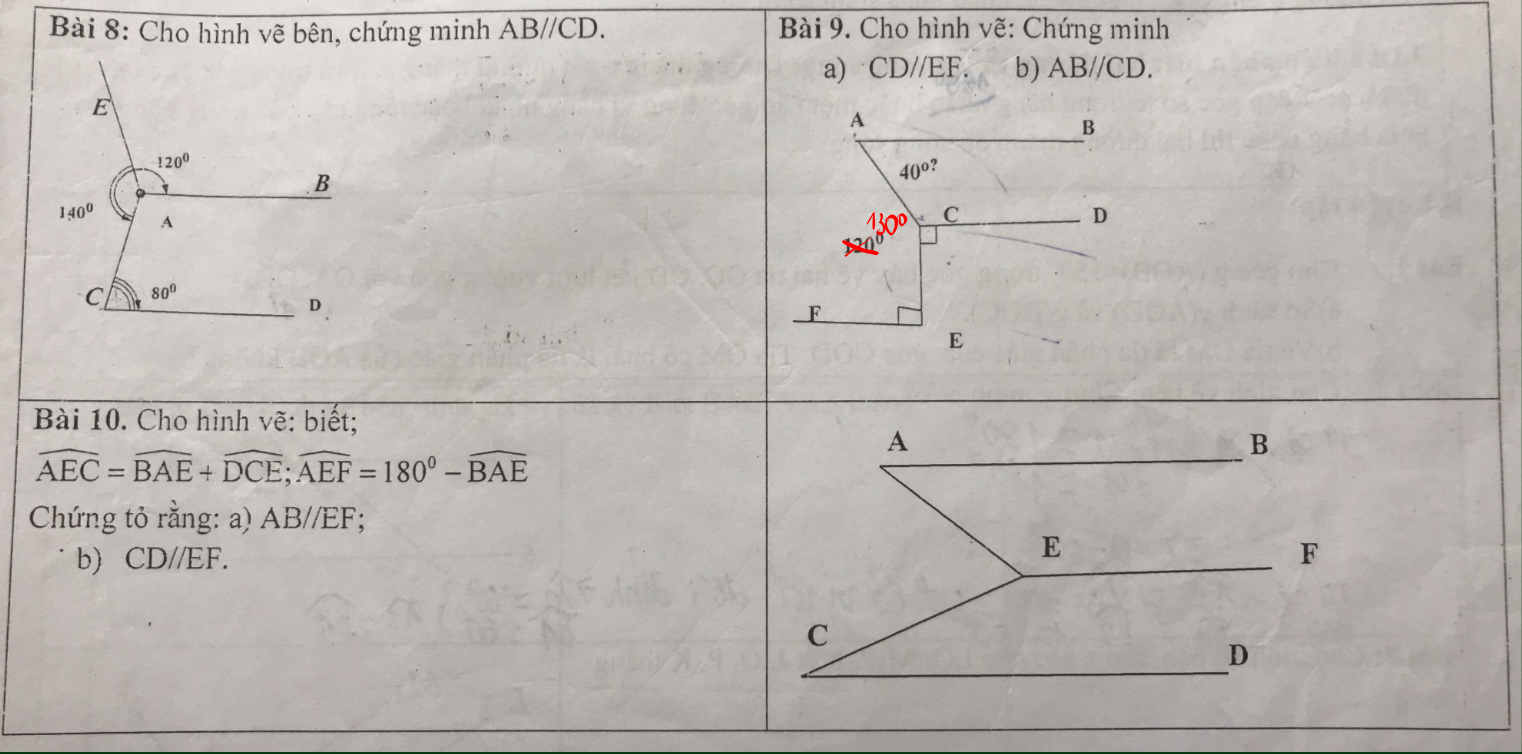
 Giúp mik mấy bài này vs
Giúp mik mấy bài này vs