Cho tam giác ABC cân tại A . Trên các cạnh AB,AC lấy lần kượt các điểm D và F sao cho AD=AE
a, Chứng minh BDEC là hình thang cân
b, Tính các góc hình thang cân đó , biết A =500
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 12 2017
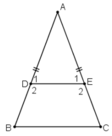
Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
10 tháng 9 2017
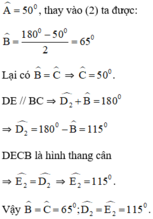
a) Ta có AD = AE nên ∆ADE cân
Do đó ˆD1= ˆE1
Trong tam giác ADE có: D1^ + ˆE1 + ˆA^=1800
Hay 2ˆD1 = 1800 - ˆA
ˆD1 = 180 độ −ˆA/2
Tương tự trong tam giác cân ABC ta có ˆB= 180−ˆA/2
Nên ˆD1 = ˆB ( hai góc đồng vị.)
Suy ra DE // BC
Do đó BDEC là hình thang.
Lại có ˆB = ˆC
Nên BDEC là hình thang cân.
b) Với ˆA=500
Ta được ˆB = ˆC = 180−ˆA/2= 180-50/2=65 độ
ˆD2=ˆE2=1800 - ˆB= 1800 - 650=1150
HH
19 tháng 6 2020
a) Ta có : AD = AE => \(\Delta ADE\)cân
\(\Rightarrow\widehat{D_1}=\widehat{E_1}\)
\(\Delta ADE\)có : \(\widehat{A}+\widehat{D_1}+\widehat{E_1}=180^o\)
Mà \(\widehat{D_1}=\widehat{E_1}\)nên \(\widehat{A}+2.\widehat{D_1}=180^o\)
\(\Rightarrow2.\widehat{D_1}=180^o-\widehat{A}\Rightarrow\widehat{D_1}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Tam giác ABC có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{B}=\widehat{C}\)( Vì tam giác ABC cân tại A )
\(\Rightarrow\widehat{A}+2.\widehat{B}=180^o\Rightarrow\widehat{B}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1)(2) => \(\widehat{D_1}=\widehat{B}\)
Mà hai góc ở vị trí đồng vị => DE // BC
=> Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
\(\widehat{A}=50^o\)thay vào (2) ta được :
\(\widehat{B}=\frac{180^o-50^o}{2}=65^o\)
Ta lại có : \(\widehat{B}=\widehat{C}\Rightarrow\widehat{C}=50^o\)
\(DE//BC\Rightarrow\widehat{D_1}+\widehat{B}=180^o\)
\(\Rightarrow\widehat{D_1}=180^o-\widehat{B}=115^o\)
DECB là hình thang cân
\(\Rightarrow\widehat{E_2}=\widehat{D_2}\Rightarrow\widehat{E_2}=115^o\)
Vậy : \(\widehat{B}=\widehat{C}=65^o\); \(\widehat{D_2}=\widehat{E_2}=115^o\)
YN
16 tháng 9 2021
a) Ta xét: Tam giác ADE có: AD = AE
=> Tam giác ADE cân tại A
\(\Rightarrow\widehat{AED}=\widehat{ACB}\)
=> DE//BC
Ta xét: Tứ giác DECB có: DE//BC
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
=> BDEC là hình thang cân
b) \(\widehat{ABC}=\frac{1}{2}\left(180^o-50^o\right)=65^o\)
\(\widehat{ACB}=\widehat{ABC}=65^o\)
\(\widehat{DEC}=180^o-65^o=115^o\)
\(\widehat{EDB}=\widehat{EDC}=115^o\)
DT
28 tháng 6 2017
Hình vẽ:
a)Xét \(\Delta ADE\) có:AD=AE(gt)
\(\Rightarrow\Delta ADE\) cân tại A
\(\Rightarrow\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\) (1)
Ta lại có:\(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{AED}=\widehat{ACB}\)
\(\Rightarrow\) DE song song với BC
Xét tứ giác DEBC có:
DE song song với BC
\(\widehat{ABC}=\widehat{ACB}\) ( 2 góc đáy của tam giác ABC cân tại A)
\(\Rightarrow\) BDEC là hình thang cân
\(\Rightarrow\widehat{BDE}=\widehat{CED}\)
b) Theo câu a có:\(\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}=\dfrac{180^o-50^o}{2}=60^0\)
mà \(\widehat{ABC}=\widehat{ACB}\) ( câu a) nên \(\widehat{ABC}=60^o\)
Vì DE song song với BC\(\Rightarrow\) góc DEC+ góc BCE=180o
=>góc DEC+60o =180o
=>góc DEC=120o mà \(\widehat{BDE}=\widehat{CED}\)
=>BDE=120o
25 tháng 8 2016
a) Ta có AD = AE nên ∆ADE cân
Do đó =
Trong tam giác ADE có: +
+
=1800
Hay 2 = 1800 -
=
Tương tự trong tam giác cân ABC ta có =
Nên =
là hai góc đồng vị.
Suy ra DE // BC
Do đó BDEC là hình thang.
Lại có =
Nên BDEC là hình thang cân.
b) Với =500
Ta được =
=
=
= 650
=1800 -
= 1800 - 650=1150
25 tháng 6 2021
a) Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(AB=AC;AD=AE\right)\)
D\(\in\)AB(gt)
E\(\in\)AC(gt)
Do đó: DE//BC(Định lí Ta lét đảo)
Xét tứ giác BDEC có DE//BC(cmt)
nên BDEC là hình thang(Định nghĩa hình thang)
Hình thang BDEC(DE//BC) có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BDEC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
1)Cho tam giác ABC cân tại A. trên các cạnh bên AB,AC lấy theo thứ tự các diểm D và E sao cho AD=AE.
a)chứng minh rằng BDEC là hình thang cân.
b)tính các góc của hình thang cân dó , biết rằng Â=50o
bài làm
a) xét tamg giác ADE có:
AD = AE => tam giác ADE cân tại A
=> AED^ = ACB^
=> DE // BC
xét tứ giác DECB có
DE // BC
ABC^ = ACB^
=> DECB là hình thang cân
b) ABC^ = 1/2 (180 - 50) = 65 độ
ACB^ = ABC = 65 độ
DEC = 180 - 65 = 115 độ
EDB = EDC = 115 độ
cách 2
a, Tam giác ABC cân tại A => AB=AC ( 1 )
theo gt AD=AE ( 2 ).
từ 1 và 2 => BD = CE. (3)
lại có AD/AB = AE/AC => DE // BC (theo talet) 4
từ 3 & 4 => BDEC là hình thang cân.
b, tam giác ABC cân tại A => góc B=C= (180-50)/2 =65.
góc BDE = CED = 180 - 65 = 115
Hình vẽ ;
a, Chứng minh tứ giác BDEC là hình thang cân.
Xét tam giác ADE ta có :
AD=AE(gt)
=> tam giác ADE cân tại A
Xét tam giác ADE cân tại A và tam giác ABC cân tại A ta có
\(\widehat{A}\)chung
=> tam giác ADE đồng dạng với tam giác ABC
=>\(\widehat{D_1}=\widehat{B_1}\)
mà hai góc này ở vị trí đồng vị
=> DE//BC
=> tứ giác BDEC là hình thang
mà \(\widehat{B}=\widehat{C}\)(do tam giác ABC cân tại A )
=> tứ giác BDEC là hình thang cân
b, Tính các góc còn lại của hình thang cân .
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=180^o-50^o=130^o\)
mà \(\widehat{B}=\widehat{C}\)( do tam giác ABC cân tại A)
=>\(\widehat{B}=\widehat{C}=\frac{130^o}{2}=65^o\)
Lại có : DE//BC(cmt)
=>\(\widehat{B}+\widehat{D_2}=180^o\Rightarrow\widehat{D_2}=180^o-\widehat{B}=180^o-65^o=115^o\)
mà \(\widehat{D_2}=\widehat{E_1}\)( do tứ giác BDEC là hình thang cân )
=>\(\widehat{E_1}=115^o\)
Nên nhớ hình vẽ chỉ mang tính minh họa cho bài làm vì vẽ trên máy tính nên ko được đẹp mấy bạn thông cảm nha .
Có j hk hiểu nhắn tin hỏi mk mình giải thích cho nhé .