Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

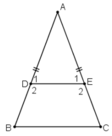
Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
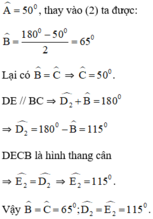

a) Ta có AD = AE nên ∆ADE cân
Do đó ˆD1= ˆE1
Trong tam giác ADE có: D1^ + ˆE1 + ˆA^=1800
Hay 2ˆD1 = 1800 - ˆA
ˆD1 = 180 độ −ˆA/2
Tương tự trong tam giác cân ABC ta có ˆB= 180−ˆA/2
Nên ˆD1 = ˆB ( hai góc đồng vị.)
Suy ra DE // BC
Do đó BDEC là hình thang.
Lại có ˆB = ˆC
Nên BDEC là hình thang cân.
b) Với ˆA=500
Ta được ˆB = ˆC = 180−ˆA/2= 180-50/2=65 độ
ˆD2=ˆE2=1800 - ˆB= 1800 - 650=1150
a) Ta có : AD = AE => \(\Delta ADE\)cân
\(\Rightarrow\widehat{D_1}=\widehat{E_1}\)
\(\Delta ADE\)có : \(\widehat{A}+\widehat{D_1}+\widehat{E_1}=180^o\)
Mà \(\widehat{D_1}=\widehat{E_1}\)nên \(\widehat{A}+2.\widehat{D_1}=180^o\)
\(\Rightarrow2.\widehat{D_1}=180^o-\widehat{A}\Rightarrow\widehat{D_1}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Tam giác ABC có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{B}=\widehat{C}\)( Vì tam giác ABC cân tại A )
\(\Rightarrow\widehat{A}+2.\widehat{B}=180^o\Rightarrow\widehat{B}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1)(2) => \(\widehat{D_1}=\widehat{B}\)
Mà hai góc ở vị trí đồng vị => DE // BC
=> Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
\(\widehat{A}=50^o\)thay vào (2) ta được :
\(\widehat{B}=\frac{180^o-50^o}{2}=65^o\)
Ta lại có : \(\widehat{B}=\widehat{C}\Rightarrow\widehat{C}=50^o\)
\(DE//BC\Rightarrow\widehat{D_1}+\widehat{B}=180^o\)
\(\Rightarrow\widehat{D_1}=180^o-\widehat{B}=115^o\)
DECB là hình thang cân
\(\Rightarrow\widehat{E_2}=\widehat{D_2}\Rightarrow\widehat{E_2}=115^o\)
Vậy : \(\widehat{B}=\widehat{C}=65^o\); \(\widehat{D_2}=\widehat{E_2}=115^o\)

a) Ta xét: Tam giác ADE có: AD = AE
=> Tam giác ADE cân tại A
\(\Rightarrow\widehat{AED}=\widehat{ACB}\)
=> DE//BC
Ta xét: Tứ giác DECB có: DE//BC
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
=> BDEC là hình thang cân
b) \(\widehat{ABC}=\frac{1}{2}\left(180^o-50^o\right)=65^o\)
\(\widehat{ACB}=\widehat{ABC}=65^o\)
\(\widehat{DEC}=180^o-65^o=115^o\)
\(\widehat{EDB}=\widehat{EDC}=115^o\)

a, Vì AD = AE nên \(\Rightarrow\Delta ADE\)là tam giác cân tại A
\(\Rightarrow gócADE\)\(=\frac{180^o-A}{2}\)
Vì \(\Delta ABC\)cân tại A nên
Góc CBA = \(\frac{180^o-A}{2}\)
\(\Rightarrow ADE=CBA\)( mà 2 góc này nằm trong vị trí so le trong )
\(\Rightarrow\)\(DE//BC\)
Mà \(ABC=ACB\)(Vì tam giác ABC cân tại A )
\(\Rightarrow\)Tứ giác BDEC là hình thang cân
b,
Ta có :
^A \(=70^o\)\(\Rightarrow\)^B=^C =\(55^O\)
\(\Rightarrow BDE=CED=\frac{\left(360-2\cdot55\right)}{2}=125^O\)

Hình vẽ:

a)Xét \(\Delta ADE\) có:AD=AE(gt)
\(\Rightarrow\Delta ADE\) cân tại A
\(\Rightarrow\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\) (1)
Ta lại có:\(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{AED}=\widehat{ACB}\)
\(\Rightarrow\) DE song song với BC
Xét tứ giác DEBC có:
DE song song với BC
\(\widehat{ABC}=\widehat{ACB}\) ( 2 góc đáy của tam giác ABC cân tại A)
\(\Rightarrow\) BDEC là hình thang cân
\(\Rightarrow\widehat{BDE}=\widehat{CED}\)
b) Theo câu a có:\(\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}=\dfrac{180^o-50^o}{2}=60^0\)
mà \(\widehat{ABC}=\widehat{ACB}\) ( câu a) nên \(\widehat{ABC}=60^o\)
Vì DE song song với BC\(\Rightarrow\) góc DEC+ góc BCE=180o
=>góc DEC+60o =180o
=>góc DEC=120o mà \(\widehat{BDE}=\widehat{CED}\)
=>BDE=120o

1)Cho tam giác ABC cân tại A. trên các cạnh bên AB,AC lấy theo thứ tự các diểm D và E sao cho AD=AE.
a)chứng minh rằng BDEC là hình thang cân.
b)tính các góc của hình thang cân dó , biết rằng Â=50o
bài làm
a) xét tamg giác ADE có:
AD = AE => tam giác ADE cân tại A
=> AED^ = ACB^
=> DE // BC
xét tứ giác DECB có
DE // BC
ABC^ = ACB^
=> DECB là hình thang cân
b) ABC^ = 1/2 (180 - 50) = 65 độ
ACB^ = ABC = 65 độ
DEC = 180 - 65 = 115 độ
EDB = EDC = 115 độ
cách 2
a, Tam giác ABC cân tại A => AB=AC ( 1 )
theo gt AD=AE ( 2 ).
từ 1 và 2 => BD = CE. (3)
lại có AD/AB = AE/AC => DE // BC (theo talet) 4
từ 3 & 4 => BDEC là hình thang cân.
b, tam giác ABC cân tại A => góc B=C= (180-50)/2 =65.
góc BDE = CED = 180 - 65 = 115
Hình vẽ ;
a, Chứng minh tứ giác BDEC là hình thang cân.
Xét tam giác ADE ta có :
AD=AE(gt)
=> tam giác ADE cân tại A
Xét tam giác ADE cân tại A và tam giác ABC cân tại A ta có
\(\widehat{A}\)chung
=> tam giác ADE đồng dạng với tam giác ABC
=>\(\widehat{D_1}=\widehat{B_1}\)
mà hai góc này ở vị trí đồng vị
=> DE//BC
=> tứ giác BDEC là hình thang
mà \(\widehat{B}=\widehat{C}\)(do tam giác ABC cân tại A )
=> tứ giác BDEC là hình thang cân
b, Tính các góc còn lại của hình thang cân .
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=180^o-50^o=130^o\)
mà \(\widehat{B}=\widehat{C}\)( do tam giác ABC cân tại A)
=>\(\widehat{B}=\widehat{C}=\frac{130^o}{2}=65^o\)
Lại có : DE//BC(cmt)
=>\(\widehat{B}+\widehat{D_2}=180^o\Rightarrow\widehat{D_2}=180^o-\widehat{B}=180^o-65^o=115^o\)
mà \(\widehat{D_2}=\widehat{E_1}\)( do tứ giác BDEC là hình thang cân )
=>\(\widehat{E_1}=115^o\)
Nên nhớ hình vẽ chỉ mang tính minh họa cho bài làm vì vẽ trên máy tính nên ko được đẹp mấy bạn thông cảm nha .
Có j hk hiểu nhắn tin hỏi mk mình giải thích cho nhé .