Tìm x: \(30x-15x^2=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(15x^4+30x^3+13x^2-2x-1=0\)
<=> \(15x^4+15x^3+15x^3+15x^2-2x^2-2x-1=0\)
<=> \(15x^2\left(x^2+x\right)+15x\left(x^2+x\right)-2\left(x^2+x\right)-1\)
<=> \(15\left(x^2+x\right)^2-2\left(x^2+x\right)-1=0\)
<=> \(\orbr{\begin{cases}x^2+x=\frac{1}{3}\\x^2+x=\frac{1}{5}\end{cases}}\)
Em tự giải tiếp nhé!


Lời giải:
$3x=16y\Rightarrow \frac{x}{16}=\frac{y}{3}$
Áp dụng TCDTSBN:
$\frac{x}{16}=\frac{y}{3}=\frac{x+y}{16+3}=\frac{190}{19}=10$
$\Rightarrow x=10.16=160; y=3.10=30$
Đáp án A.


a) \(8x^2+30x+7=0\)
\(\Leftrightarrow8\left(x^2+\frac{15}{4}x+7\right)=0\)
\(\Leftrightarrow x^2+\frac{1}{4}x+\frac{7}{2}x+\frac{7}{8}=0\)
\(\Leftrightarrow x\left(x+\frac{1}{4}\right)+\frac{7}{2}\left(x+\frac{1}{4}\right)=0\)
\(\Leftrightarrow\left(x+\frac{1}{4}\right)\left(x+\frac{7}{2}\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x+\frac{1}{4}=0\\x+\frac{7}{2}=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-\frac{1}{4}\\x=-\frac{7}{2}\end{array}\right.\)
b)\(x^3-11x^2+30x=0\)
\(\Leftrightarrow x\left(x^2-11x+30\right)=0\)
\(\Leftrightarrow x\left(x^2-5x-6x+30\right)=0\)
\(\Leftrightarrow x\left[x\left(x-5\right)-6\left(x-5\right)\right]=0\)
\(\Leftrightarrow x\left(x-5\right)\left(x-6\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=0\\x-5=0\\x-6=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=0\\x=5\\x=6\end{array}\right.\)
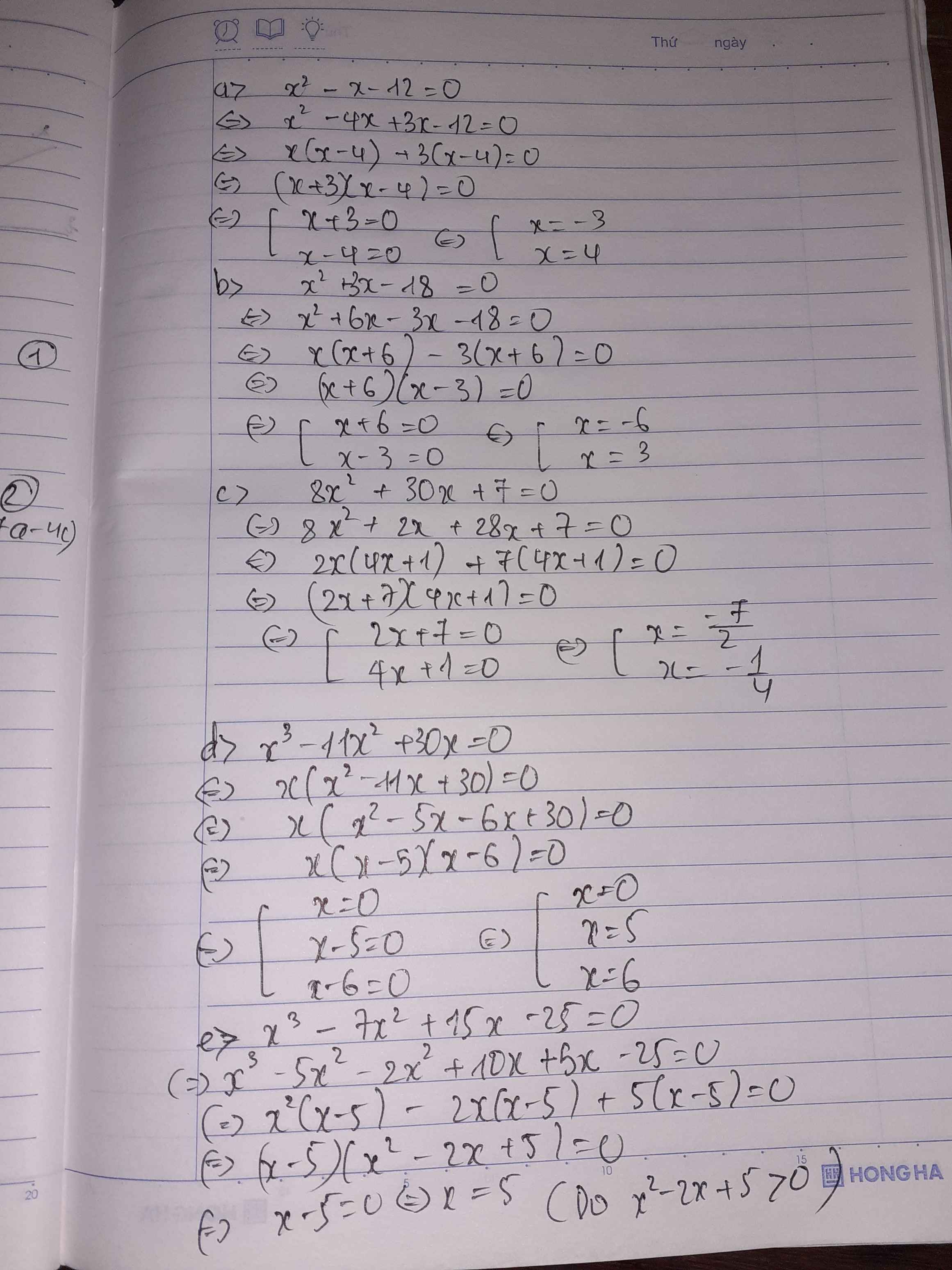
\(30x-15x^2-0\)
\(\Leftrightarrow15x\left(2-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}15x=0\\2-x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)