Tính tổng các cạnh của một hình hộp chữ nhật, biết rằng thể tích của chúng bằng \(a^3\), diện tích toàn phần của nó bằng \(2ma^2\) và các cạnh lập thành một cấp số nhân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi a, b, c là ba kích thước của hình hộp chữ nhật.
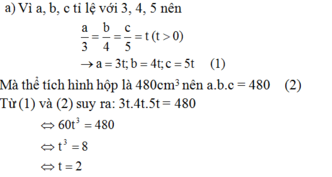
Vậy các kích thước của hình chữ nhật là: 6cm; 8cm; 10cm.


a, diện tích xung quanh là
8 * 8 * 4 = 256 (cm2)
diện tích toàn phần là
8 * 8 * 6 = 384 (cm2)
thể tích là
8 * 8 * 8 = 512 (cm3)
b, tự nghĩ

Tổng của chiều dài và chiều rộng của hình lập phương là :
26 : 2 = 13 ( dm )
Chiều rộng của hình hộp chữ nhật là :
( 13 - 5 ) : 2 = 4 ( dm )
Chiều dài của hình hộp chữ nhật là :
4 + 5 = 9 ( dm )
Diện tích đáy hình hộp hình chữ nhật là :
9 x 4 = 36 ( dm2 )
Vì thể tích hai hình bằng nhau , có chiều cao bằng nhau nên diện tích đáy bằng nhau . Vậy diện tích đáy của hình lập phương là 36 dm2 .
Vì 36 = 6 x 6 nên cạnh của hình lập phương là 6 dm .
Thể tích của hình lập phương là :
6 x 6 x 6 = 216 ( dm3 )
Vì chiều cao hình hộp hình chữ bằng cạnh hình lập phương nên chiều cao hình hộp hình chữ nhật là 6 dm .
Diện tích xung quanh hình hộp hình chữ nhật là :
26 x 6 = 156 ( dm2 )
Diện tích toàn phần hình hộp hình chữ nhật là :
156 + 36 x 2 = 228 ( dm2 )
Đáp số : Thể tích hình lập phương : 216 dm3
Diện tích toàn phần hình hộp chữ nhật : 228 m2

1.
TBC tổng các số ghi trang sách là: 1810 : 20 = 90,5
Số cuối cùng của 10 trang phần đầu là: 90,5 - 0,5 = 90
Trang đầu tiên của phần sách đó là: 90 - (10 -1) = 81
ĐS: 81
2.
HHCN có diện tích toàn phần nhỏ nhất khi xếp các hình lập phương nhỏ thành HHCN có 3 kích thước là: 3 x 2 x 2.
Diện tích 2 đáy là: 3 x 2 x 2 = 12 cm2
Diện tích xuing quanh là: (3 + 2) x 2 x 2 = 20 cm2
Diện tích toàn phần là: 12 + 20 = 32 cm2
ĐS: 32 cm2

thể tích của hình lập phương là:
\(8.8.8=512\left(cm^3\right)\)
chiều cao của hình hộp cn là:
\(512:16:8=4\left(cm\right)\)
diện tích xung quanh hình hộp là:
\(\left(16+8\right).2.4=192\left(cm^2\right)\)
diện tích toàn phần của hình hộp là:
\(192+16.8.2=448\left(cm^2\right)\)
Thể tích hình hộp là:
\(8^3=512\left(cm^3\right)\)
Chiều cao là 512:16:8=32:8=4(cm)
Diện tích xung quanh là:
(16+8)x2x4=192(cm2)
Diện tích toàn phần là:
192+2x16x8=192+256=448(cm2)


Do các cạnh của hình hộp chữ nhật là một cấp số nhân nên đặt q là công bội của cấp số nhân ta có lần lượt các cạnh là: \(x;xq;xq^2\)
Theo đề bài ta có: \(\left\{{}\begin{matrix}x\cdot xq\cdot xq^2=a^3\\2\cdot x\cdot\left(xq+xq^2\right)+2\cdot xq\cdot xq^2=2ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^3q^3=a^3\\2x\cdot\left(xq+xq^2\right)+2x^2q^3=2ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xq=a\\2xq\left(x+xq\right)+2x^2q^3=2ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xq=a\\2a\left(x+a\right)+2a^2q=2ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xq=a\\2ax+2a^2+2a^2q=2ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xq=a\\ax+a^2+a^2q=ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xq=a\\x+a+aq=ma\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\cdot aq=a^2\\x+aq=a\left(m-1\right)\end{matrix}\right.\)
Khi đó x và aq chính là nghiệm của pt:
\(t^2-a\left(m-1\right)t+a^2=0\)
\(\sqrt{\Delta}=\sqrt{\left[-a\left(m-1\right)\right]^2-4\cdot1\cdot a^2}=\sqrt{a^2\left(m^2-2m+1\right)-4a^2}\\ =\sqrt{a^2m^2-2ma^2+a^2-4a^2}=a\sqrt{m^2-2m-3}\\ =a\sqrt{\left(m-3\right)\left(m+1\right)}\)
\(\Leftrightarrow\left[{}\begin{matrix}t_1=\dfrac{a\left(m-1\right)+a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\\t_2=\dfrac{a\left(m-1\right)-a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\end{matrix}\right.\)
Với \(\left\{{}\begin{matrix}x=\dfrac{a\left(m-1\right)+a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\\aq=\dfrac{a\left(m-1\right)-a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{a\left(m-1\right)+a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\\q=\dfrac{\left(m-1\right)-\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\end{matrix}\right.\)
\(\Rightarrow x+xq+xq^2=....\)
Với: \(\left\{{}\begin{matrix}x=\dfrac{a\left(m-1\right)-a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\\aq=\dfrac{a\left(m-1\right)+a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{a\left(m-1\right)-a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\\q=\dfrac{\left(m-1\right)+\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\end{matrix}\right.\)
\(\Rightarrow x+xq+xq^2=...\)