Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Gọi x là chiều dài đoạn thép thứ nhất, 0 < x < 10
=> Cạnh hình tứ diện là (tứ diện là đều)
Cạnh hình lập phương là 10 - x 12
Diện tích xung quanh của tứ diện là ![]()
Diện tích xung quanh của lập phương là ![]()
Tổng
S
1
+
S
2
đạt giá trị nhỏ nhất khi 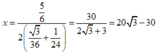
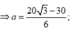
![]()
![]()

Đáp án B
Ta có
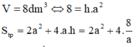
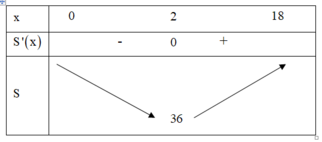
Ta tìm điều kiện của a đê diện tích toàn phần nhỏ nhất. xét hàm số ta được a=2

Gọi ba số đã cho u1,u2,u7 theo thứ tự là ba số của một cấp số cộng (un) và v1,v2, v3 của cấp số nhân (vn) . Theo giả thiết Ta có hệ:
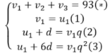
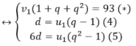
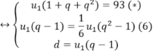
Giải phương trình (6)
( 6 ) ⇔ u 1 q − 1 = 1 6 u 1 q − 1 q + 1 ⇔ u 1 q − 1 = 0 ( l o a i ) 1 = 1 6 q + 1
Thay vào (*), ta được
u 1 1 + 5 + 5 2 = 93 ⇔ u 1 = 3 = v 1
Suy ra
u 2 = u 1 . q = 3.5 = 15 = v 2 u 3 = u 1 . q 2 = 3.25 = 75 = v 3
Vậy tích ba số v 1 . v 2 . v 3 = 3.15.75 = 3375
Đáp án A
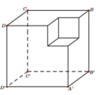
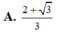


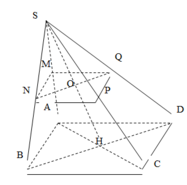
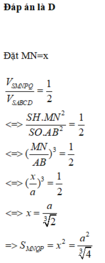



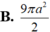
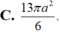
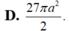
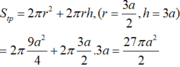

Do các cạnh của hình hộp chữ nhật là một cấp số nhân nên đặt q là công bội của cấp số nhân ta có lần lượt các cạnh là: \(x;xq;xq^2\)
Theo đề bài ta có: \(\left\{{}\begin{matrix}x\cdot xq\cdot xq^2=a^3\\2\cdot x\cdot\left(xq+xq^2\right)+2\cdot xq\cdot xq^2=2ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^3q^3=a^3\\2x\cdot\left(xq+xq^2\right)+2x^2q^3=2ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xq=a\\2xq\left(x+xq\right)+2x^2q^3=2ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xq=a\\2a\left(x+a\right)+2a^2q=2ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xq=a\\2ax+2a^2+2a^2q=2ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xq=a\\ax+a^2+a^2q=ma^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xq=a\\x+a+aq=ma\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\cdot aq=a^2\\x+aq=a\left(m-1\right)\end{matrix}\right.\)
Khi đó x và aq chính là nghiệm của pt:
\(t^2-a\left(m-1\right)t+a^2=0\)
\(\sqrt{\Delta}=\sqrt{\left[-a\left(m-1\right)\right]^2-4\cdot1\cdot a^2}=\sqrt{a^2\left(m^2-2m+1\right)-4a^2}\\ =\sqrt{a^2m^2-2ma^2+a^2-4a^2}=a\sqrt{m^2-2m-3}\\ =a\sqrt{\left(m-3\right)\left(m+1\right)}\)
\(\Leftrightarrow\left[{}\begin{matrix}t_1=\dfrac{a\left(m-1\right)+a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\\t_2=\dfrac{a\left(m-1\right)-a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\end{matrix}\right.\)
Với \(\left\{{}\begin{matrix}x=\dfrac{a\left(m-1\right)+a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\\aq=\dfrac{a\left(m-1\right)-a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{a\left(m-1\right)+a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\\q=\dfrac{\left(m-1\right)-\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\end{matrix}\right.\)
\(\Rightarrow x+xq+xq^2=....\)
Với: \(\left\{{}\begin{matrix}x=\dfrac{a\left(m-1\right)-a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\\aq=\dfrac{a\left(m-1\right)+a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{a\left(m-1\right)-a\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\\q=\dfrac{\left(m-1\right)+\sqrt{\left(m+1\right)\left(m-3\right)}}{2}\end{matrix}\right.\)
\(\Rightarrow x+xq+xq^2=...\)