 giúp mình với ạ mình cần gấp
giúp mình với ạ mình cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


PTHH : 2Al + 6HCl --> 2AlCl3 + 3H2 ↑ (1)
nAlCl3 = \(\dfrac{m}{M}=\dfrac{13,35}{27+35,5.3}=0.1\left(mol\right)\)
Từ (1) => nHCl = 2nH2 = 0.2 (mol)
=> mHCl = n.M = 0.2 x 36.5 = 7.3 (g)
\(PTHH:2Al+6HCl\rightarrow2AlCl_3+3H_2\\ n_{AlCl_3}=\dfrac{m}{M}=\dfrac{13,35}{133,5}=0,1\left(mol\right)\\ Theo.PTHH:n_{HCl}=3.n_{AlCl_3}=3.0,1=0,3\left(mol\right)\\ m_{HCl}=n.M=0,3.36,5=10,95\left(g\right)\)

Câu 4 :
\(n_{Fe2O3}=\dfrac{24}{160}=0,15\left(mol\right)\)
Pt : \(Fe_2O_3+3H_2SO_4\rightarrow Fe_2\left(SO_4\right)_3+3H_2O|\)
1 3 1 3
0,15 0,15
a) \(n_{Fe2\left(SO4\right)3}=\dfrac{0,15.1}{1}=0,15\left(mol\right)\)
⇒ \(m_{Fe2\left(SO4\right)3}=0,15.400=60\left(g\right)\)
b) \(C_{M_{Fe2\left(SO4\right)3}}=\dfrac{0,15}{0,5}=0,3\left(M\right)\)
Chúc bạn học tốt
a,\(n_{Fe_2O_3}=\dfrac{24}{160}=0,15\left(mol\right)\)
PTHH: Fe2O3 + 3H2SO4 → Fe2(SO4)3 + 3H2O
Mol: 0,15 0,45 0,15
\(m_{Fe_2\left(SO_4\right)_3}=0,15.400=60\left(g\right)\)
b,\(C_{M_{ddFe_2\left(SO_4\right)_3}}=\dfrac{0,15}{0,5}=0,3\left(mol\right)\)

A. MgSO4
- Liên kết ion được hình thành bởi cation kim loại Mg2+ và anion gốc axit SO42-
- Liên kết cộng hóa trị giữa S và O.
A: MgSO4
Liên kết ion giữa Mg2+ và SO42-, liên kết cộng hóa trị giữa S và O

Có:
\(m=\dfrac{F_{hd}R^2}{GM}=\dfrac{F'_{hd}\left(R+h\right)^2}{GM}\)
\(\Leftrightarrow F_{hd}R^2=F'_{hd}\left(R+h\right)^2\)
\(\Leftrightarrow45R^2=5\left(R^2+h^2+2Rh\right)\)
\(\Leftrightarrow45R^2=5R^2+5h^2+10Rh\)
\(\Leftrightarrow45R^2-5R^2-5h^2-10Rh=0\)
\(\Leftrightarrow40R^2-5h^2-10Rh=0\)
\(\Leftrightarrow h=12800km\)


a: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=x+4\)
=>\(x^2=2x+8\)
=>\(x^2-2x-8=0\)
=>(x-4)(x+2)=0
=>\(\left[{}\begin{matrix}x-4=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
Thay x=4 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot4^2=\dfrac{1}{2}\cdot16=8\)
Thay x=-2 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)
Vậy: A(4;8); B(-2;2)
b: Ta có: A(4;8)
=>Tọa độ hình chiếu của A trên trục Ox là:
\(\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)
=>H(4;0)
B(-2;2)
Tọa độ hình chiếu của B trên Ox là:
\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
=>K(-2;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}x=0\\y=0+4=4\end{matrix}\right.\)
Vậy: C(0;4)
H(4;0); K(-2;0)
\(CO=\sqrt{\left(0-0\right)^2+\left(4-0\right)^2}=4\)
\(HK=\sqrt{\left(-2-4\right)^2+\left(0-0\right)^2}=\sqrt{6^2+0}=6\)
Diện tích ΔCHK là:
\(S_{CHK}=\dfrac{1}{2}\cdot CO\cdot HK=\dfrac{1}{2}\cdot4\cdot6=2\cdot6=12\)

b: Xét ΔCAB vuông tại A và ΔCAE vuông tại A có
CA chung
AB=AE
Do đó: ΔCAB=ΔCAE
Suy ra: \(\widehat{BCA}=\widehat{ECA}\)
hay CA là tia phân giác của \(\widehat{BCE}\)



 Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé
Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé 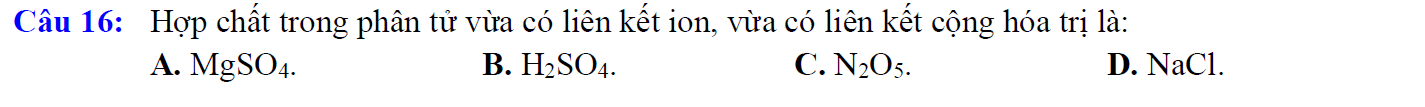 Giúp mình với ạ, mình đang cần gấp ạ
Giúp mình với ạ, mình đang cần gấp ạ




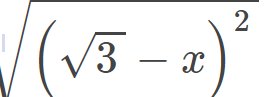
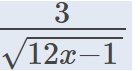 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
x O y t A m C B
a/
\(\widehat{xOt}=\widehat{tOy}=\dfrac{\widehat{xOy}}{2}=\dfrac{60^o}{2}=30^o\)
b/
\(\widehat{xAm}=\widehat{xOy}=60^o\)
Hai góc trên ở vị trí đồng vị => Am//Oy
c/
Ta có
Am//Oy (cmt) \(\Rightarrow\widehat{ACO}=\widehat{tOy}\) (góc so le trong)
BC//Ox (gt) \(\Rightarrow\widehat{BCO}=\widehat{xOt}\) (góc so le trong)
Mà \(\widehat{xOt}=\widehat{tOy}\left(cmt\right)\)
\(\Rightarrow\widehat{ACO}=\widehat{BCO}\)