Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Xét t giác ABC cân tại A có AH là đường cao
=> AH là đường phân giác
=> góc EAH= góc FAH
xét Δ AEH và Δ AFH có
góc AEH= góc AFH = 90 độ
góc EAH= góc FAH
chung AH
=> Δ AEH = Δ AFH ( cạnh huyền - góc nhọn)
b, Xét Δ AEH = Δ AFH=> AE= AF
xét Δ AEF có AE= AF => Δ AEF cân tại A
Xét Δ AEF cân tại A có AH là đường phân giác
=> AH cũng là trung trực
=> AH là trung trực của EF (đpcm)
c, có ME= EH=> E là tđ của MH
Có AE ⊥ MH tại tđ E của MH
=> AE là trung trực của MH
=> AM= AH (1)
có FH= FN=> F là tđ của HN
Có AF ⊥ HN tại tđ F của HN
=> AF là trung trực của HN
=> AH= AN (2)
Từ (1) và (2) => AM= AN
=> Δ AMN cân tại A
a: Xét ΔAEH vuông tại E và ΔAFH vuông tại F có
AH chung
góc EAH=góc FAH
Do đó: ΔAEH=ΔAFH
b: Ta có: AE=AF
HE=HF
Do đó: AH là đường trung trực của FE
c: Xét ΔAHM có
AE là đường cao
AE là đường trung tuyến
Do đo ΔAHM can tại A
=>AH=AM(1)
Xét ΔAHN có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔAHN cân tại A
=>AH=AN(2)
Từ (1) và (2) suy ra AM=AN
Gọi O là giao của EF và AH, K là giao AM và EF
Vì \(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\) nên AEHF là hcn
Do đó \(OE=OF=OH=OA\)
\(\Rightarrow\Delta AOF\) cân tại O \(\Rightarrow\widehat{AFO}=\widehat{FAO}\left(1\right)\)
Vì AM là trung tuyến ứng với cạnh huyền BC nên \(AM=BM=CM=\dfrac{1}{2}BC\)
\(\Rightarrow\Delta AMC\) cân tại M \(\Rightarrow\widehat{MCA}=\widehat{MAC}\left(2\right)\)
Vì tam giác AHC vuông tại H nên \(\widehat{MCA}+\widehat{FAO}=90^0\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\widehat{MAC}+\widehat{AFO}=90^0\)
Mà \(\widehat{AFO}+\widehat{MAC}+\widehat{AKF}=180^0\Rightarrow\widehat{AKF}=90^0\)
Vậy AM vuông góc EF
a: góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hcn
b: ΔHAB vuông tại H có HE vuông góc AB
nên AE*AB=AH^2
ΔAHC vuông tại H có HF vuông góc AC
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
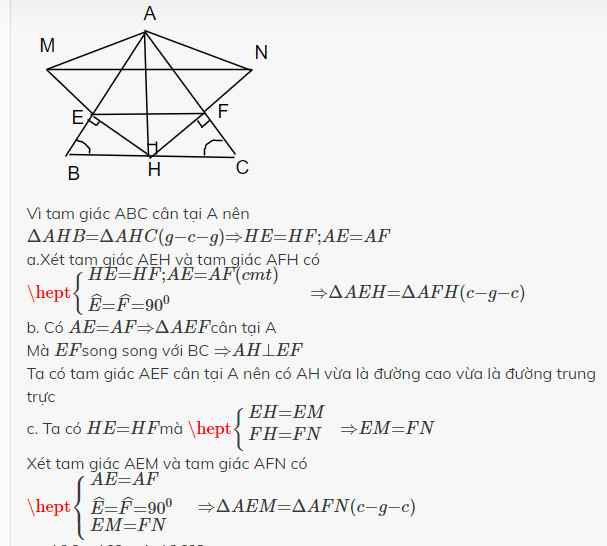
Vì tam giác ABC cân tại A nên \(\Delta AHB=\Delta AHC\left(g-c-g\right)\Rightarrow HE=HF;AE=AF\)
a.Xét tam giác AEH và tam giác AFH có \(\hept{\begin{cases}HE=HF;AE=AF\left(cmt\right)\\\widehat{E}=\widehat{F}=90^0\end{cases}\Rightarrow\Delta AEH=\Delta AFH}\left(c-g-c\right)\)
b. Có \(AE=AF\Rightarrow\Delta AEF\)cân tại A
Mà \(EF\)song song với BC \(\Rightarrow AH⊥EF\)
Ta có tam giác AEF cân tại A nên có AH vừa là đường cao vừa là đường trung trực
c. Ta có \(HE=HF\)mà \(\hept{\begin{cases}EH=EM\\FH=FN\end{cases}}\)\(\Rightarrow EM=FN\)
Xét tam giác AEM và tam giác AFN có \(\hept{\begin{cases}AE=AF\\\widehat{E}=\widehat{F}=90^0\\EM=FN\end{cases}}\Rightarrow\Delta AEM=\Delta AFN\left(c-g-c\right)\)
\(\Rightarrow AM=AN\Rightarrow\Delta AMN\)cân tại A