Tìm số có hai chữ số,biết nếu thêm đằng trước và sau chữ số đó số 4 sau đó cộng với số cần tìm thì bằng 4387
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số phải tìm là abcde
Ta có phép nhân
abcde7
x 4
=7abcde
Lần lượt tìm các chữ số
7x4 có tận cùng là e =>e=8 nhớ 2
4e+2 có tận cùng bằng d =>d=4 nhớ 3
4d +3 có tận cùng bằng c =>c=9 nhớ 1
4c +1 có tận cùng bằng b =>b=7 nhớ 3
4b +3 có tận cùng bằng a =>a=1 nhớ 3
4a +3 có tận cùng bằng 7 (đúng với kết quả vừa tìm)
Vậy abcde=17948
thử lại 179487x4=717948

Gọi số cần tìm là abc (a khác 0 ; a,b,c là chữ số)
Ta có : 4abc - abc4 = 2889
=> 4000 + abc - 2889 = abc x 10 + 4
=> 1111 + abc = abc x 10 + 4
Cùng bớt abc + 4 được :
1107 = abc x 9
=> abc = 1107 : 9 = 123
Vậy số cần tìm là 123

Bài 1:
Số có 5 chữ số có dạng: \(\overline{abcde}\)
Khi viết thêm chữ số 2 vào đằng sau số đó ta được số mới là:
\(\overline{abcde2}\)
Khi viết thêm chữ số 2 vào đằng trước số đó ta được số mới là: \(\overline{2abcde}\)
Theo bài ra ta có: \(\overline{abcde2}\) = \(\overline{2abcde}\) \(\times\) 3
10\(\times\)\(\overline{abcde}\) + 2 = (200000 + \(\overline{abcde}\))\(\times\) 3
\(\overline{abcde}\) \(\times\)10 + 2 = 600000 + \(\overline{abcde}\)\(\times\) 3
\(\overline{abcde}\) \(\times\) 10 - \(\overline{abcde}\) \(\times\) 3 = 600000 - 2
\(\overline{abcde}\) \(\times\) ( 10 - 3) = 599998
7\(a\) = 599998
\(a\) = 599998: 7
\(a\) = 85714
Bài 2: Số có hai chữ số có dạng: \(\overline{ab}\)
Khi viết thêm chữ số 1 vào bên trái số và bên phải số đó ta có số mới là: \(\overline{1ab1}\)
Theo bài ra ta có: \(\overline{1ab1}\) = \(\overline{ab}\) \(\times\) 23
1001 + \(\overline{ab}\) \(\times\) 10 = \(\overline{ab}\) \(\times\) 23
\(\overline{ab}\) \(\times\) 23 - \(\overline{ab}\) \(\times\) 10 = 1001
\(\overline{ab}\) \(\times\)(23 - 10) = 1001
\(\overline{ab}\) \(\times\) 13 = 1001
\(\overline{ab}\) = 1001: 13
\(\overline{ab}\) = 77
Kết luận: Số thỏa mãn đề bài là 77

17: Gọi số cần tìm là X
Theo đề, ta có: 1000+10x+1=23X
=>13X=1001
=>X=77
16:
Gọi số cần tìm là X
Theo đề, ta có: \(10X+2=3\left(200000+X\right)\)
=>7X=600000-2=599998
=>X=85714

Giả sử số tự nhiên có dạng $\overline{abcde}$.
Ta cần tìm chữ số $a$.
Khi ta thêm số 7 vào đằng trước số $\overline{abcde}$, ta được số: $\overline{7abcde}$.
Khi ta thêm số 7 vào sau số $\overline{abcde}$, ta được số: $\overline{abcde7}$.
Theo đề bài, ta có: $\overline{7abcde} = 4\times\overline{abcde7}$ Suy ra: $70000 + \overline{abcde} = 4(10\overline{abcde} +7)$ $70000 + \overline{abcde} = 40\overline{abcde} + 28$ $69972 = 39\overline{abcde}$ $\overline{abcde} = 1794$
Vậy số tự nhiên cần tìm là: $\boxed{17947}$.

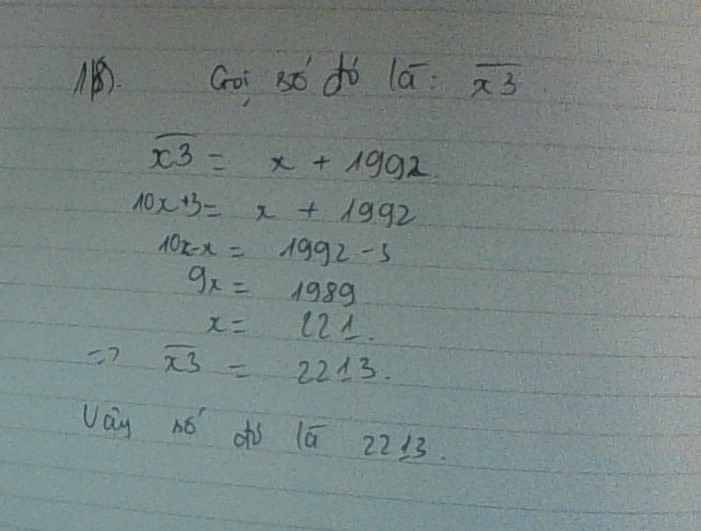
Thầy thử làm thì không tìm ra số thoả mãn, em xem lại đề
Dạ thầy