Cho h/c SABCD có đáy ABCD là hình thang vuông tại A, B, SA⊥(ABCD), AD=2a, AB=BC=a
cm: a) CD⊥(SAC)
b) CD⊥ SC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2023
a.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}=\left(SB;\left(ABCD\right)\right)\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SBA}\approx35^016'\)
Tương tự \(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=\left(SC;\left(ABCD\right)\right)\)
\(AC=\sqrt{AD^2+DC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow\left(AH;\left(SAD\right)\right)=90^0-\left(AH;AB\right)=90^0-\widehat{HAB}\)
Gọi E là trung điểm AB \(\Rightarrow ADCE\) là hình vuông \(\Rightarrow\widehat{ACE}=45^0\)
Tam giác BCE vuông cân tại E (do \(EB=EC=a\)) nên \(\widehat{ECB}=45^0\)
\(\Rightarrow\widehat{ACB}=90^0\) hay \(BC\perp AC\Rightarrow BC\perp\left(SAC\right)\) (do \(SA\perp BC\))
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp BH\)
Hay tam giác ABH vuông tại H
\(AH=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
\(\Rightarrow cos\widehat{HAB}=\dfrac{AH}{AB}=\dfrac{1}{2}\Rightarrow\widehat{HAB}=60^0\)
\(\Rightarrow\widehat{HAB}=60^0\Rightarrow\left(AH;\left(SAD\right)\right)=30^0\)
Theo cmt \(BC\perp\left(SAC\right)\Rightarrow\left(SB;\left(SAC\right)\right)=\widehat{BSC}\)
\(SC=\sqrt{SA^2+AC^2}=2a\) ; \(SB=\sqrt{SA^2+AB^2}=a\sqrt{6}\)
\(\Rightarrow cos\widehat{BSC}=\dfrac{SC}{SB}=\dfrac{\sqrt{6}}{3}\Rightarrow\widehat{BSC}\approx35^016'\)
8 tháng 4 2023
a: \(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1/căn 2
=>góc SCA=35 độ
b:
Kẻ BH vuông góc AC tại H
(SB;SAC)=(SB;SH)=góc BSH
\(HB=\dfrac{a\cdot a}{a\sqrt{2}}=a\cdot\dfrac{\sqrt{2}}{2}\)
AH=AC/2=a*căn 2/2
=>\(SH=\sqrt{a^2+\dfrac{1}{2}a^2}=a\sqrt{\dfrac{3}{2}}\)
\(SH=\dfrac{a\sqrt{6}}{2};HB=\dfrac{a\sqrt{2}}{2};SB=a\sqrt{2}\)
\(cosBSH=\dfrac{SB^2+SH^2-BH^2}{2\cdot SB\cdot SH}=\dfrac{\sqrt{3}}{2}\)
=>góc BSH=30 độ
c: (SD;(SAB))=(SD;SA)=góc ASD
tan ASD=AD/AS=2
nên góc ASD=63 độ
HP
19 tháng 6 2021
Ta có: \(S_{ABCD}=\dfrac{\left(BC+AD\right).AB}{2}=\dfrac{3}{2}a^2\)
a, \(h=SA=AB.tan60^o=a\sqrt{3}\)
\(\Rightarrow V=\dfrac{1}{3}.S_{ABCD}.h=\dfrac{1}{3}.\dfrac{3}{2}a^2.a\sqrt{3}=\dfrac{\sqrt{3}}{2}a^3\)
b, \(h=SA=AD.tan45^o=2a\)
\(\Rightarrow V=\dfrac{1}{3}.S_{ABCD}.h=\dfrac{1}{3}.\dfrac{3}{2}a^2.2a=a^3\)
c, Dễ chứng minh được SC vuông góc với CD tại C \(\Rightarrow\widehat{SCA}=30^o\)
\(\Rightarrow h=SA=AC.tan30^o=AD.sin45^o.tan30^o=\dfrac{\sqrt{6}}{3}a\)
\(\Rightarrow V=\dfrac{1}{3}.S_{ABCD}.h=\dfrac{1}{3}.\dfrac{3}{2}a^2.\dfrac{\sqrt{6}}{3}a=\dfrac{\sqrt{6}}{6}a^3\)
CM
3 tháng 7 2018
Đáp án B
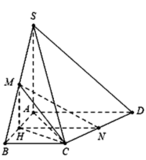
Dễ thấy 
Gọi H là trung điểm của AB 
Tam giác MHN vuông tại H, có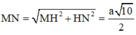 
Tam giác MHC vuông tại H, có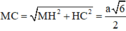 
Tam giác MNC, có
c
o
s
M
N
C
^
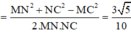
Vậy cos(MN;(SAC)) = sin M N C ^ = 1 - cos 2 M N C ^ = 55 10
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2021
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) ; mà \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\)
\(\left\{{}\begin{matrix}CD\perp\left(SAD\right)\Rightarrow CD\perp AK\\AK\perp SD\end{matrix}\right.\) \(\Rightarrow AK\perp\left(SCD\right)\)
\(\left\{{}\begin{matrix}AH\perp\left(SBC\right)\Rightarrow AH\perp SC\\AK\perp\left(SCD\right)\Rightarrow AK\perp SC\end{matrix}\right.\) \(\Rightarrow SC\perp\left(AHK\right)\Rightarrow SC\perp HK\)
Mặt khác theo tính đối xứng hình vuông \(\Rightarrow HK||BD\Rightarrow HK\perp AC\Rightarrow HK\perp\left(SAC\right)\)
\(AI\in\left(SAC\right)\Rightarrow HK\perp AI\)
a: ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(AC^2=a^2+a^2=2a^2\)
=>\(AC=a\sqrt{2}\)
Xét ΔADC có \(cosDAC=\dfrac{AD^2+AC^2-CD^2}{2\cdot AD\cdot AC}\)
=>\(cos45=\dfrac{2a^2+4a^2-CD^2}{2\cdot a\sqrt{2}\cdot2a}\)
=>\(6a^2-CD^2=4a^2\cdot\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=4a^2\)
=>\(CD^2=2a^2\)
=>\(CD=a\sqrt{2}\)
Xét ΔCAD có \(CA^2+CD^2=AD^2\)
nên ΔCAD vuông tại C
=>CA\(\perp\)CD
CD\(\perp\)CA
CD\(\perp\)SA
SA,CA cùng thuộc mp(SAC)
Do đó: CD\(\perp\)(SAC)
b: CD\(\perp\)(SAC)
\(SC\subset\left(SAC\right)\)
Do đó: CD\(\perp\)SC