Tìm giá trị của m để bất phương trình x2 + 2mx - 2m +3 ≥ 0 có tập nghiệm R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 4 2021
- Trước tiên ta tìm điều kiện của mm để phương trình đã cho có hai nghiệm phân biệt: x1,x2(Δ′>0)x1,x2(Δ′>0).
- Ta biến đổi biểu thức 2(x12+x22)−5x1x22(x12+x22)−5x1x2 về biểu thức có chứa x1+x2x1+x2 và x1x2x1x2 rồi từ đó ta tìm được giá trị của mm.
- Đối chiếu với điều kiện xác định của mm để tìm được giá trị thỏa mãn yêu cầu của bài toán.
CM
31 tháng 12 2017
Phương trình x 2 – 2mx + 2m − 1 = 0 có a = 1 ≠ 0 và = 4 m 2 – 4 (2m – 1)
= 4 m 2 – 8 m + 4 = 4 ( m – 1 ) 2 ≥ 0 ; ∀ m
Phương trình có hai nghiệm x 1 ; x 2 với mọi m
Theo hệ thức Vi-ét ta có x 1 + x 2 = 2 m x 1 . x 2 = 2 m − 1
Xét
x 1 2 + x 2 2 = x 1 + x 2 2 - 2 x 1 x 2 ⇔ 4 m 2 – 2 ( 2 m – 1 ) = 10
⇔ 4 m 2 – 4 m + 2 – 10 = 0 ⇔ 4 m 2 – 4 m – 8 = 0 ⇔ m 2 – m – 2 = 0
m 2 – 2 m + m – 2 = 0 ⇔ m ( m – 2 ) + ( m – 2 ) = 0 ⇔ ( m + 1 ) ( m – 2 ) = 0
⇔ m = 2 m = − 1
Vậy m = 2 và m = −1 là các giá trị cần tìm
Đáp án: D
14 tháng 5 2023
Δ=(2m)^2-4(m^2+2m+3)
=4m^2-4m^2-8m-12=-8m-12
Để PT có 2 nghiệm pb thì -8m-12>0
=>-8m>12
=>m<-3/2
x1^3+x2^3=108
=>(x1+x2)^3-3x1x2(x1+x2)=108
=>(-2m)^3-3(m^2+2m+3)*(-2m)=108
=>-8m^3+6m(m^2+2m+3)=108
=>-8m^3+6m^3+12m^2+18m-108=0
=>-2m^3+12m^2+18m-108=0
=>-2m^2(m-6)+18(m-6)=0
=>(m-6)(-2m^2+18)=0
=>m=-3
2
29 tháng 5 2023
Ptr có nghiệm `<=>\Delta' > 0`
`<=>(-m)^2-2m+1 > 0`
`<=>(m-1)^2 > 0<=>m-1 ne 0<=>m ne 1`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=2m),(x_1.x_2=c/a=2m-1):}`
Ta có: `(x_1 ^2-2mx_1 +3)(x_2 ^2-2mx_2 -2)=50`
`<=>[x_1 ^2-(x_1+x_2)x_1+3][x_2 ^2-(x_1+x_2)x_2 -2]=50`
`<=>(-x_1.x_2+3)(-x_1.x_2-2)=50`
`<=>(1-2m+3)(1-2m-2)=50`
`<=>(4-2m)(-1-2m)=50`
`<=>-4-8m+2m+4m^2=50`
`<=>4m^2-6m-54=0`
`<=>4m^2+12m-18m-54=0`
`<=>(m+3)(4m-18)=0<=>[(m=-3),(m=9/2):}` (t/m)
AH
Akai Haruma
Giáo viên
1 tháng 4 2021
PT $(*)$ là PT bậc nhất ẩn $x$ thì làm sao mà có $x_1,x_2$ được hả bạn?
PT cuối cũng bị lỗi.
Bạn xem lại đề!
XO
2 tháng 5 2023
Phương trình đã cho có nghiệm phân biệt khi :
\(\Delta'=m^2-\left(m^2+2m+3\right)=-2m-3>0\)
\(\Leftrightarrow m< -\dfrac{3}{2}\)(*)
Hệ thức Viette : \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=m^2+2m+3\end{matrix}\right.\)
Có \(x_1^3+x_2^3=108\)
\(\Leftrightarrow\left(x_1+x_2\right).\left(x_1^2-x_1x_2+x_2^2\right)=108\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=108\)
\(\Leftrightarrow-8m^3+6m\left(m^2+2m+3\right)=108\)
\(\Leftrightarrow m^3-6m^2-9m+54=0\)
\(\Leftrightarrow\left(m-6\right).\left(m-3\right).\left(m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=6\\m=\pm3\end{matrix}\right.\)
Kết hợp (*) được m = -3 thỏa mãn
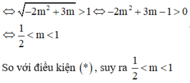
\(x^2+2mx-2m+3>=0\)(1)
\(\text{Δ}=\left(2m\right)^2-4\cdot1\cdot\left(-2m+3\right)\)
\(=4m^2+8m-12\)
\(=4\left(m^2+2m-3\right)=4\left(m+3\right)\left(m-1\right)\)
Để bất phương trình (1) đúng với mọi x thuộc R thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4\left(m+3\right)\left(m-1\right)< =0\\1>0\end{matrix}\right.\)
=>\(\left(m+3\right)\left(m-1\right)< =0\)
TH1: \(\left\{{}\begin{matrix}m+3>0\\m-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-3\\m< 1\end{matrix}\right.\)
=>-3<m<1
TH2: \(\left\{{}\begin{matrix}m+3< 0\\m-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -3\\m>1\end{matrix}\right.\)
=>\(m\in\varnothing\)