giúp mình câu c, d với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 10 2021
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2021
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
ND
Nguyễn Đức Trí
VIP
18 tháng 9 2023
a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)
QD
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
1
KV
29 tháng 11 2023
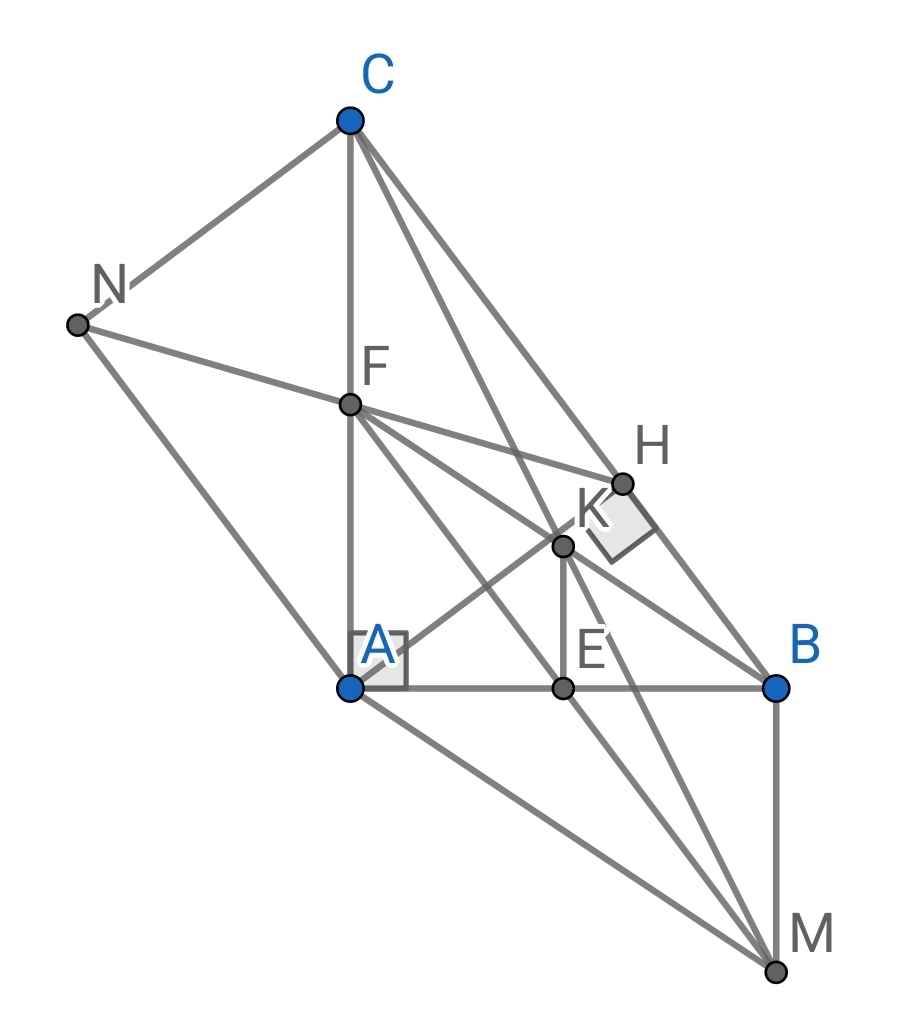c) Do AMBF là hình bình hành (cmt)
⇒ BM // AF
Mà AF ⊥ AB
⇒ BM ⊥ AB
⇒ ∠ABM = 90⁰
Do AHCN là hình chữ nhật (cmt)
⇒ ∆AHC vuông tại H
F là trung điểm của AC (gt)
⇒ HF = AF = CF = AC : 2
⇒ ∆AHF cân tại F
⇒ ∠AHF = ∠FAH
Mà ∠FAH + ∠HAB = 90⁰
⇒ ∠AHF + ∠HAB = 90⁰
Lại có:
∆AHB vuông tại H
⇒ ∠HAB + ∠HBA = 90⁰
Mà ∠HAB + ∠AHF = 90⁰ (cmt)
⇒ ∠AHF = ∠HBA (1)
Do ∠FHB = ∠AHF + ∠AHB
= ∠AHF + 90⁰ (2)
∠MBH = ∠HBA + ∠ABM
= HBA + 90⁰ (3)
Từ (1), (2), (3) ⇒ ∠FHB = ∠MBH
∆ABC có:
E là trung điểm của AB (gt)
F là trung điểm của AC (gt)
⇒ EF // BC
⇒ FM // BH
Tứ giác BMFH có:
FM // BH (cmt)
⇒ BMFH là hình thang
Mà ∠FHB = ∠MBH (cmt)
⇒ BMFH là hình thang cân
KV
29 tháng 11 2023
d)
Do AMBF là hình bình hành (cmt)
⇒ AF = BM và AF // BM
Do F là trung điểm của AC (gt)
⇒ AF = CF = AC : 2
⇒ AC = 2AF
Mà AF = BM (cmt)
⇒ CF = BM
Do AF // BM (cmt)
⇒ CF // BM
Tứ giác BCFM có:
CF // BM (cmt)
CF = BM (cmt)
⇒ BCFM là hình bình hành
Mà K là giao điểm của BF và CM (gt)
⇒ K là trung điểm của BF
∆FBM có:
K là trung điểm của BF (cmt)
E là trung điểm của FM (gt)
⇒ EK là đường trung bình của BM
⇒ EK = BM : 2
⇒ BM = 2EK
Do AHCN là hình chữ nhật (cmt)
⇒ AC = HN
Lại có AC = 2AF (cmt)
⇒ HN = 2AF
Mà AF = BM
⇒ HN = 2BM
Mà BM = 2EK
⇒ HN = 2.2EK = 4EK
Vậy HN = 4EK
17 tháng 12 2021
c.
\(n_A=\dfrac{5,6}{22,4}=0,25\left(mol\right)\)
\(\Rightarrow m_A=0,25.32=8\left(g\right)\)
\(n_{CO_2}=\dfrac{28}{22,4}=1,25\left(mol\right)\)
\(\Rightarrow m_{CO_2}=1,25.44=55\left(g\right)\)
d.
\(V_{O_2}=0,25.22,4=5,6\left(l\right)\)
\(V_{CO_2}=0,1.22,4=2,24\left(l\right)\)
17 tháng 12 2021
bn sửa hộ mik \(n_A\Rightarrow n_{O_2}\), \(m_A\Rightarrow m_{O_2}\) nhé, vừa nãy mik nhìn nhầm
10 tháng 10 2021
a: Xét ΔHAB có
I là trung điểm của HA
M là trung điểm của HB
Do đó: IM là đường trung bình của ΔHAB
Suy ra: IM//AB
hay ABMI là hình thang
NH
1
12 tháng 8 2023
`@` `\text {Ans}`
`\downarrow`
`c)`
\(2-3^{x-1}-7=11\)
`\Rightarrow`\(3^{x-1}-5=11\)
`\Rightarrow`\(3^{x-1}=11+5\)
`\Rightarrow`\(3^{x-1}=16\)
Bạn xem lại đề
`d)`
\(\left(x-\dfrac{3}{5}\right)\div\dfrac{-1}{3}=-0,4\)
`\Rightarrow`\(x-\dfrac{3}{5}=-0,4\cdot\left(-\dfrac{1}{3}\right)\)
`\Rightarrow`\(x-\dfrac{3}{5}=\dfrac{2}{15}\)
`\Rightarrow`\(x=\dfrac{2}{15}+\dfrac{3}{5}\)
`\Rightarrow`\(x=\dfrac{11}{15}\)
Vậy, \(x=\dfrac{11}{15}\)
Bạn nên viết lại đề cho rõ ràng để nhận được sự trợ giúp tốt hơn nhé.