cho x+y=1 tìm giá trị nhỏ nhất M=x3+y3+2xy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$

Ta có: T = x 3 + y 3 − x 2 + y 2 x − 1 y − 1 = x 2 x − 1 + y 2 y − 1 x − 1 y − 1 = x 2 y − 1 + y 2 x − 1
Do x > 1 , y > 1 nên x − 1 > 0 , y − 1 > 0
Áp dụng bất đẳng thức Cauchy cho 2 số dương x 2 y − 1 , y 2 x − 1 ta có:
x − 1 + 1 ≥ 2 x − 1 ⇔ x − 1 − 1 2 ≥ 0 ⇔ x − 2 x − 1 ≥ 0 ⇔ x x − 1 ≥ 2 y − 1 + 1 ≥ 2 y − 1 ⇔ y − 1 − 1 2 ≥ 0 ⇔ y − 2 y − 1 ≥ 0 ⇔ x y − 1 ≥ 2
Do đó: T = x 2 y − 1 + y 2 x − 1 ≥ 2 x y x − 1 . y − 1 ≥ 8
Dấu “=” xẩy ra khi x 2 y − 1 = y 2 x − 1 x − 1 = 1 y − 1 = 1 ⇔ x = 2 y = 2 (thỏa mãn điều kiện)
Vậy giá trị nhỏ nhất của biểu thứcT= 8 khi x=y= 2
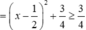


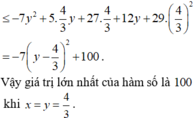
Lời giải:
$M=x^3+y^3+2xy=(x+y)(x^2-xy+y^2)+2xy=x^2-xy+y^2+2xy$
$=x^2+y^2+xy=\frac{1}{4}(x-y)^2+\frac{3}{4}(x+y)^2=\frac{1}{4}(x-y)^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$. Giá trị này đạt được khi $x=y=\frac{1}{2}$