Chứng tỏ rằng: (am)n = am.n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 6 2019
Lưu ý đây là vẽ hình bình hành mong bn thông cảm mik vẽ xấu vl
a, Ta có :
AM=MB=AB2;CN=ND=CD2;AB=CDAM=MB=AB2;CN=ND=CD2;AB=CD
⇒AM=MB=CN=ND⇒AM=MB=CN=ND
Mà AB=2AD=BCAB=2AD=BC hay AD=AM=MB=CN=ND=BCAD=AM=MB=CN=ND=BC
Xét tứ giác MBCN ,có :
BM= CN ( c/mt )
BM // CN ( AB // CD )
=> MBCN là hình bình hành
mà MB = BC
=> MBCN là hình thoi
=> MC⊥BNMC⊥BN
b, C/m tương tự , ta có : Tứ giác AMND cũng là hình thoi
⇒⇒ MD là phân giác của góc AMN
⇒AMNˆ=2DMNˆ⇒AMN^=2DMN^
BMNC là hình thoi
=> MC là phân giác của góc BMN
=> BMNˆ=2CMNˆBMN^=2CMN^
Ta có : AMNˆ+BMNˆ=1800AMN^+BMN^=1800
Hay 2DMNˆ+2CMNˆ=18002DMN^+2CMN^=1800
⇒DMNˆ+CMNˆ=900⇒DMN^+CMN^=900
Hay DMCˆ=900
CT
2
VM
14 tháng 11 2019
Đề phải cho là \(\widehat{B}=\widehat{C}=\) bao nhiêu độ nữa chứ? cà thái thành
CM
31 tháng 12 2018
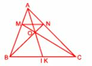
a) Vì AB = 3 x AM, AC = 3 x AN, nên MB = 2/3 x AB, NC = 2/3 x AC.
Từ đó suy ra : dt (MBC) = 2/3 x dt (ABC) (chung chiều cao từ C
dt (NCB) = 2/3 x dt (ABC) (chung chiều cao từ B)
Vậy dt (MBC) = dt (NCB) mà tam giác MBC và tam giác NCB có chung đáy BC, nên chiều cao từ M bằng chiều cao từ N xuống đáy BC hay MN song song với BC. Do đó BMNC là hình thang.
Từ MB = 2/3 x AB, nên dt (MBN) = 2/3 x dt (ABN) (chung chiều cao từ N) hay dt (ABN) = 2/3 x dt (MBN).
Hơn nữa từ AC = 3 x AN, nên NC = 2 x AN, do đó dt (NBC) = 2 x dt (ABN) (chung chiều cao từ B) ; suy ra dt (NBC) = 3/2 x 2 x dt (MBN) = 3 x dt (MBN).
Mà tam giác NBC và tam giác MBN có chiều cao bằng nhau (cùng là chiều cao của hình thang BMNC). Vì vậy đáy BC = 3 x MN.
b) Gọi BN cắt CM tại O. Ta sẽ chứng tỏ AI cũng cắt BN tại O. Muốn vậy, nối AO kéo dài cắt BC tại K, ta sẽ chứng tỏ K là điểm chính giữa của BC (hay K trùng với I).
Theo phần a) ta đã có dt (NBC) = 2 x dt (ABN). Mà tam giác NBC và tam giác ABN có chung đáy BN, nên chiều cao từ C gấp 2 lần chiều cao từ A xuống đáy BN. Nhưng đó là chiều cao tương ứng của hai tam giác BCO và BAO có chung đáy BO, vì vậy dt (BCO) = 2 x dt (BAO)
Tương tự ta cũng có dt (BCO) = 2 x dt (CAO).
Do đó dt (BAO) = dt (CAO). Hai tam giác BAO và CAO có chung đáy AO, nên chiều cao từ B bằng chiều cao từ C xuống đáy AO. Đó cũng là chiều cao tương ứng của hai tam giác BOK và COK có chung đáy OK, vì vậy dt (BOK) = dt (COK). Mà hai tam giác BOK và tam giác COK lại chung chiều cao từ O, nên hai đáy BK = CK hay K là điểm chính giữa của cạnh BC. Vậy điểm K trùng với điểm I hay BN, CM, AI cùng cắt nhau tại điểm O.
28 tháng 11 2016
de ma minh moi hoc hom qua xong de toi di hoc ve minh gui loi giai cho
4 tháng 12 2017
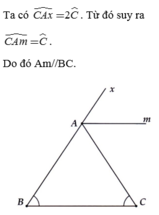
Giả sử góc ngoài tại đỉnh A là xAC
Ta có: BÂC = 180 độ - (góc B + góc C) = 180 độ - 100 độ = 80 độ => xÂC = 180 - 80 = 100 độ
Mà Am là tia p/g của xÂC => xÂm = mÂC = xÂC : 2 = 100 : 2 = 50 độ
Vì mÂC và góc BCA là hai góc so le trong nên => Am// BC
18 tháng 11 2015
a, ta có AN=AB-BN=5-1=4cm
do đó AM<AN [vi 2<4] suy ra M nằm giữa 2 điểm A và N
b,ta có MN=AN-AM=4-2=2cm
bạn thử thay số vào
VD:(2^2)^3=64
2^2.3=2^6=64
Câu hỏi của Nguyễn Thị Trà My - Toán lớp 6 - Học toán với OnlineMath
Bác tham khảo ở đây đi!