42. Cho tam giác ABC có AC = 2AB đường phân giác AD. Vẽ điểm E sao cho B là trung điểm của CE. Chứng minh rằng hat DAE = 90 deg
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 11 2021
a: Xét ΔEAB và ΔDAC có
EA=DA
AB=AC
EB=DC
Do đó: ΔEAB=ΔDAC
Suy ra: \(\widehat{EAB}=\widehat{DAC}\)
27 tháng 8 2022
Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
27 tháng 11 2016
Giải:
a) Vì \(\Delta ABC\) có AB = AC nên \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{B_2}=\widehat{C_1}\)
\(\Rightarrow180^o-\widehat{B_2}=180^o-\widehat{C_1}\)
hay \(\widehat{DBE}-\widehat{B_2}=\widehat{ECD}-\widehat{C_1}\)
\(\Rightarrow\widehat{B_1}=\widehat{C_2}\) (*)
Xét \(\Delta ABD,\Delta ACE\) có:
\(AB=AC\left(gt\right)\)
\(\widehat{B_1}=\widehat{C_2}\) ( theo (*) )
\(BD=CE\left(gt\right)\)
\(\Rightarrow\Delta ABD=\Delta ACE\left(c-g-c\right)\)
\(\Rightarrow AD=AE\) ( cạnh t/ứng ) (đpcm)
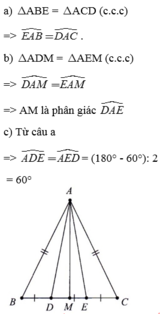
b) Ta có: \(BM=MC\left(=\frac{1}{2}BC\right)\)
\(BD=CE\left(gt\right)\)
\(\Rightarrow BM+BD=MC+CE\)
\(\Rightarrow MD=ME\) (**)
Xét \(\Delta DAM,\Delta MAE\) có:
\(AD=AE\) ( theo phần a )
\(MD=ME\) ( theo (**) )
\(AM\): cạnh chung
\(\Rightarrow\Delta DAM=\Delta MAE\left(c-c-c\right)\)
\(\Rightarrow\widehat{DAM}=\widehat{MAE}\) ( góc t/ứng )
\(\Rightarrow AM\) là tia phân giác của \(\widehat{DAE}\left(đpcm\right)\)
Vậy...
27 tháng 11 2016
Ta có hình vẽ
a/ Ta có: \(\widehat{ABC}\)=\(\widehat{ACB}\) (vì \(\Delta\)ABC cân) (*)
Mà \(\widehat{ABC}\)+\(\widehat{ABD}\)=1800 (kề bù) (**)
và \(\widehat{ACB}\)+\(\widehat{ACE}\)=1800 (kề bù) (***)
Từ (*),(**),(***) => \(\widehat{ABD}\) = \(\widehat{ACE}\) (1)
Ta có: AB = AC (GT) (2)
BD = CE (GT) (3)
Từ (1),(2),(3) => tam giác ABD = tam giác ACE
=> AD = AE (2 cạnh tương ứng) (đpcm)
b/ Xét tam giác AMD và tam giác AME có:
AD = AE (đã chứng minh ở câu a)
AM: cạnh chung
\(\begin{cases}BM=MC\\BD=CE\end{cases}\)\(\Rightarrow\) MB+BD=MC+CE \(\Rightarrow\)MD = ME
=> tam giác AMD = tam giác AME (c.c.c)
=> \(\widehat{DAM}\)=\(\widehat{EAM}\) (2 góc tương ứng)
=> AM là phân giác góc DAE (đpcm)
11 tháng 3 2023
1:
AB=1/2AC=AM=MC
=>AB=2AE=2EM=MC
Xet ΔABC và ΔAEB có
AB/AE=AC/AB=2
góc A chung
=>ΔABC đồng dạng với ΔAEB
2: AM=AB
=>ΔAMB cân tại A
mà AG là phân giác
nên AG vuông góc BM và AG là đường trung tuyến ứng với cạnh MB
Xét ΔBAM có
BE,AG là trung tuyến
=>G là trọng tâm
3: CM/ME=2
CD/DB=2
=>CM/ME=CD/DB
=>MD//BG
=>MD/BE=CM/CE=2/3
=>MD=2/3BE=BG
=>BDMG làhình bình hành
mà GB=GM(G là trọng tâm của ΔAMB cân tại A)
nên BDMG là hình thoi
8 tháng 7 2021
a) Xét ΔAND và ΔCNB có
NA=NC(N là trung điểm của AC)
\(\widehat{AND}=\widehat{CNB}\)(hai góc đối đỉnh)
ND=NB(N là trung điểm của BD)
Do đó: ΔAND=ΔCNB(c-g-c)
b) Ta có: ΔAND=ΔCNB(cmt)
nên AD=BC(hai cạnh tương ứng)
Ta có: ΔAND=ΔCNB(cmt)
nên \(\widehat{ADN}=\widehat{CBN}\)(hai góc tương ứng)
mà \(\widehat{ADN}\) và \(\widehat{CBN}\) là hai góc ở vị trí so le trong
nên AD//BC(Dấu hiệu nhận biết hai đường thẳng song song)
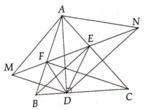
Ta có
\(AC=2AB\Rightarrow AB=\dfrac{AC}{2}\)
Gọi K là trung điểm AC
\(\Rightarrow AK=CK=\dfrac{AC}{2}\)
\(\Rightarrow AB=AK\) => tg ABK cân tại A
Ta có
\(\widehat{BAD}=\widehat{CAD}\) (gt)
\(\Rightarrow AD\perp BK\) (trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao) (1)
Xét tg ACE có
AK=CK; BE=BC (gt) => BK là đường trung bình của tg ACE
=> BK//AE (2)
Từ (1) và (2) => \(AD\perp AE\Rightarrow\widehat{DAE}=90^o\) (Hai đường thẳng // nếu đường thẳng thứ 3 vuông góc với 1 trong 2 đường thẳng cho trước thì vuông góc với đường thẳng còn lại)