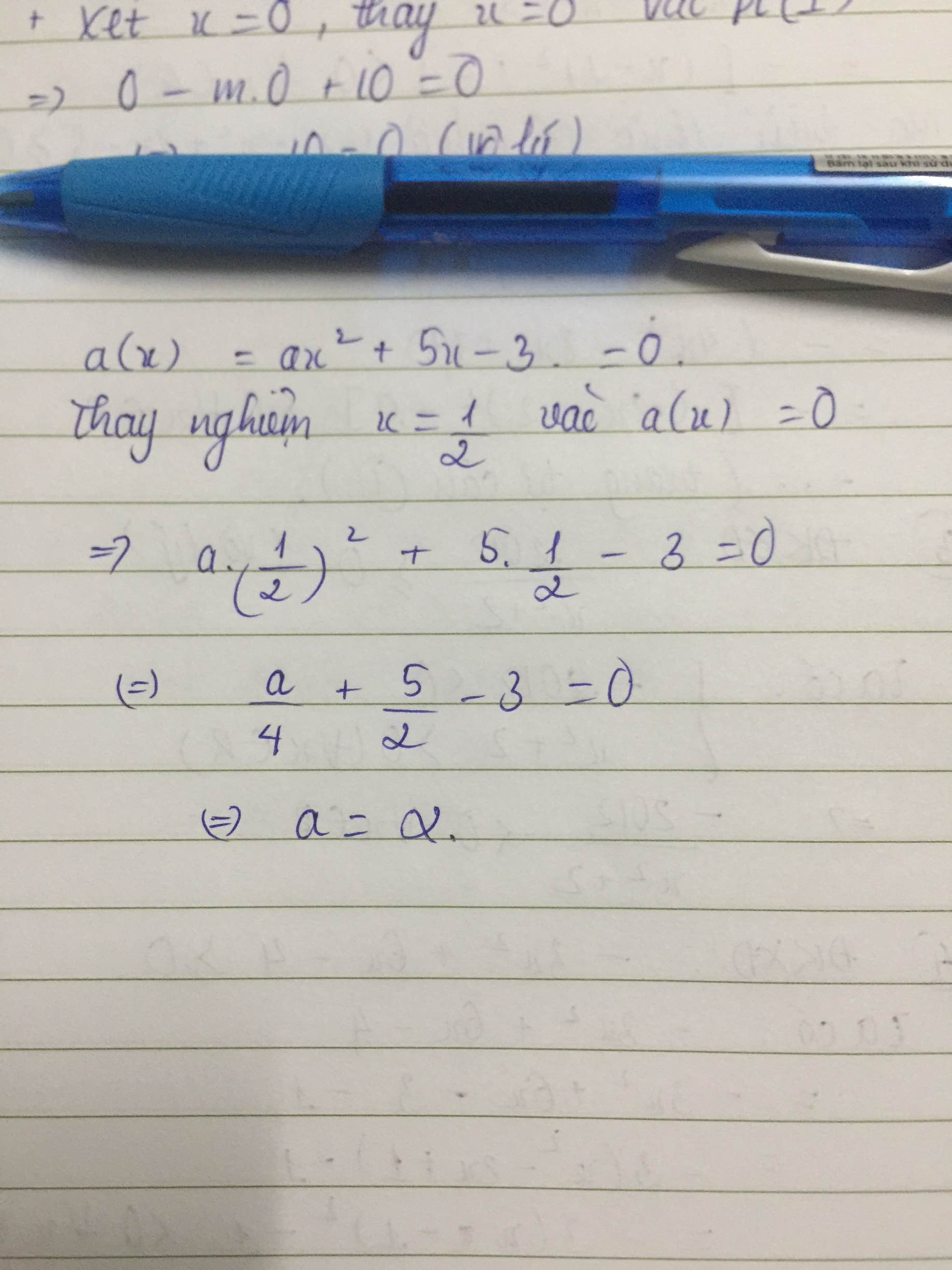Tìm hệ số a của đa thức P(x)=ax+5 biết rằng P(-3)=-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NQ
1
KK
27 tháng 3 2018
Vì đa thức \(M_{\left(x\right)}=ax^2+5-3\) có nghiệm là \(\frac{1}{2}\) nên:
\(M\left(\frac{1}{2}\right)=0\Leftrightarrow a\left(\frac{1}{2}\right)^2+5-3=0\)
\(\Rightarrow a.\frac{1}{4}+2=0\)
\(\Rightarrow a.\frac{1}{4}=-2\)
\(\Rightarrow a=-2\div\frac{1}{4}\)
\(\Rightarrow a=-8\)
NA
Nguyễn An Ninh
VIP
6 tháng 5 2023
a) Ta có f(7) = a7 + b và f(2) + f(3) = (a2+ b) + (a3 + b) = 5a + 2b. Vậy để f(7) = f(2) + f(3), ta cần giải phương trình:
a7 + b = 5a + 2b
Simplifying, ta được: 2a = b.
Vậy điều kiện của a và b để f(7) = f(2) + f(3) là b = 2a.
b) Để tìm nghiệm của P(x), ta cần giải phương trình (x-2)(2x+5) = 0:
(x-2)(2x+5)= 0
→ X-2 = 0 hoặc 2x+5 = 0
→ x = 2 hoặc x = -5/2
Vậy nghiệm của P(x) là x = 2 hoặc x =-5/2.
c) Ta biết rằng đa thức P(x) có 1 nghiệm là -2, vậy ta có thể viết P(x)
dưới dạng:
P(x) = (x+2)(x^3 - 2x^2 + ax - 2)
Từ đó suy ra:
P(-2) = (-2+2)(8 - 4a - 2) = 0
⇔-8a= 16
⇔a = -2
Vậy hệ số a của P(x) là -2.
HT
1
14 tháng 4 2016
THAY X=A/2 VÀO ĐA THỨC TA CÓ
M(X)=a*1/4+5*1/2-3=0
vậy a=2
NT
3
P
7 tháng 5 2015
P(x) = ax^2 + 5x - 3
Đa thức này có một nghiệm là 1/2 tức là P(1/2) = 0
=> a/4 + 5/2 - 3 = 0
=> a = 2
Đáp số: a = 2
J
2
9 tháng 4 2016
P(x) = ax2 + 5x - 3
Đa thức này có một nghiệm là 1/2 tức là P(1/2) = 0
=> a/4 + 5/2 - 3 = 0
=> a = 2
Đáp số: a = 2
9 tháng 4 2016
P(x) = ax^2 + 5x - 3
Đa thức này có một nghiệm là 1/2 tức là P(1/2) = 0
=> a/4 + 5/2 - 3 = 0
=> a = 2
Đáp số: a = 2
MT
3
