cứu emm vs ạaa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
6 tháng 1
Bài 2:
\(a,\dfrac{-1}{3}.\dfrac{5}{7}=\dfrac{-5}{21}\\ b,\dfrac{1}{2}.\dfrac{-3}{4}=\dfrac{-3}{8}\\ c,\dfrac{19}{7}.\dfrac{7}{15}=\dfrac{19.1}{1.15}=\dfrac{19}{15}\\ d,\dfrac{5}{11}:\left(-9\right)=\dfrac{5}{11}.\dfrac{-1}{9}=\dfrac{-5}{99}\\ e,-1:\dfrac{3}{5}=-1.\dfrac{5}{3}=-\dfrac{5}{3}\\ f,\dfrac{-2}{9}:\dfrac{2}{9}:\dfrac{-9}{14}=-\left(\dfrac{2}{9}:\dfrac{2}{9}\right).\dfrac{-14}{9}=-1.\dfrac{-14}{9}=\dfrac{14}{9}\\ k,\left(-\dfrac{2}{7}\right)^2=\left(-1\right)^2.\left(\dfrac{2}{7}\right)^2=1.\dfrac{2^2}{7^2}=\dfrac{4}{49}\\ l,\dfrac{1}{3}.\left(\dfrac{1}{3}\right)^3=\left(\dfrac{1}{3}\right)^4=\dfrac{1^4}{3^4}=\dfrac{1}{243}\\ m,\left(-\dfrac{1}{2}\right)^2.\left(\dfrac{1}{2}\right)^3=\left(-1\right)^2.\left(\dfrac{1}{2}\right)^{2+3}=1.\left(\dfrac{1}{2}\right)^5=1.\dfrac{1^5}{2^5}=\dfrac{1}{32}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
6 tháng 1
Bài 1:
\(a,\dfrac{1}{-8}+\dfrac{-5}{8}=\dfrac{-1}{8}+\dfrac{-5}{8}=\dfrac{-\left(1+5\right)}{8}=-\dfrac{6}{8}=\dfrac{-6:2}{8:2}=-\dfrac{3}{4}\\ b,\dfrac{1}{7}+\dfrac{-3}{7}=\dfrac{1-3}{7}=-\dfrac{2}{7}\\ c,\dfrac{-12}{35}+\dfrac{-7}{35}=\dfrac{-\left(12+7\right)}{35}=\dfrac{-19}{35}\\ d,\dfrac{1}{6}+\dfrac{2}{5}=\dfrac{1.5+2.6}{6.5}=\dfrac{5+12}{30}=\dfrac{17}{30}\\ e,\dfrac{3}{5}+\dfrac{-7}{4}=\dfrac{3.4-7.5}{5.4}=\dfrac{12-35}{20}=\dfrac{-23}{20}\\ g,-2-\left(-\dfrac{1}{5}\right)=-2+\dfrac{1}{5}=\dfrac{-2.5+1}{5}=\dfrac{-9}{5}\\ h,\dfrac{2}{3}-\left(-1\right)=\dfrac{2}{3}+1=\dfrac{5}{3}\\ i,4-\dfrac{2}{3}=\dfrac{4.3-2}{3}=\dfrac{12-2}{3}=\dfrac{10}{3}\\ j,\dfrac{3}{4}-2=\dfrac{3-2.4}{4}=\dfrac{-5}{4}\\ k,-1-\left(-\dfrac{2}{3}\right)=-1+\dfrac{2}{3}=\dfrac{-1.3+2}{3}=\dfrac{-3+2}{3}=-\dfrac{1}{3}\)
AH
Akai Haruma
Giáo viên
14 tháng 7 2023
Đề mờ quá. Bạn nên gõ đề ra để mọi người hỗ trợ tốt hơn nhé.
HN
0
10 tháng 1
Bài 1:
\(A=3+3^2+...+3^{100}\)
=>\(3\cdot A=3^2+3^3+...+3^{101}\)
=>\(3A-A=3^2+3^3+...+3^{101}-3-3^2-...-3^{100}\)
=>\(2A=3^{101}-3\)
=>\(2A+3=3^{101}\)
mà \(2A+3=3^n\)
nên n=101
Bài 2:
a: \(M=3+3^2+3^3+3^4+...+3^{100}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{99}+3^{100}\right)\)
\(=\left(3+3^2\right)+3^2\left(3+3^2\right)+...+3^{98}\left(3+3^2\right)\)
\(=12\left(1+3^2+...+3^{98}\right)⋮12\)
=>\(M=4\cdot3\cdot\left(1+3^2+...+3^{98}\right)⋮4\)
b: \(M=3+3^2+...+3^{100}\)
=>\(3M=3^2+3^3+...+3^{101}\)
=>\(3M-M=3^2+3^3+...+3^{101}-3-3^2-...-3^{100}\)
=>\(2M=3^{101}-3\)
=>\(2M+3=3^{101}\)
=>n=101
8 tháng 12 2021
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
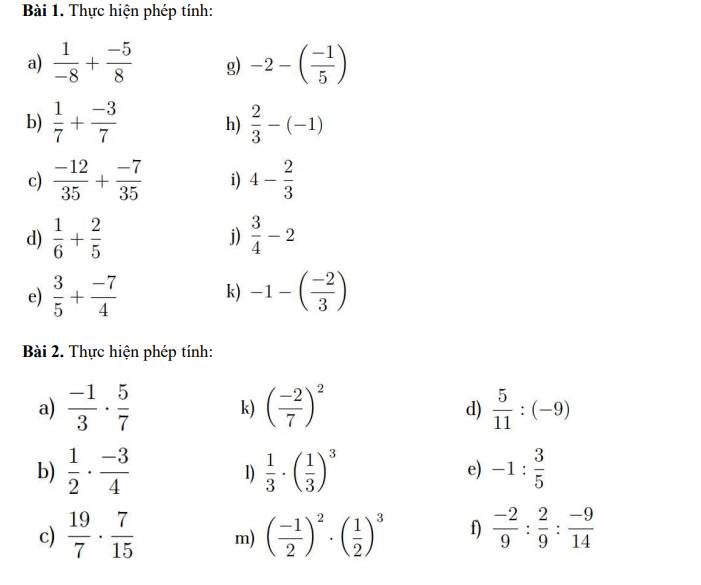
giúp em vs ạaa
Bài 1:
a: \(k=\dfrac{y}{x}=\dfrac{y_1}{x_1}=\dfrac{2}{3}\)
=>\(y=\dfrac{2}{3}x\)
b: Khi \(x_2=9\) thì \(y_2=\dfrac{2}{3}\cdot x_2=\dfrac{2}{3}\cdot9=6\)
c: Khi \(y_3=8\) thì \(\dfrac{2}{3}\cdot x_3=8\)
=>\(x_3=8:\dfrac{2}{3}=12\)
Bài 2:
a: x,y tỉ lệ thuận
nên \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{6}{y_2}=\dfrac{4}{9}\)
=>\(y_2=6\cdot\dfrac{9}{4}=\dfrac{3}{2}\cdot9=\dfrac{27}{2}\)
b: \(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\)
=>\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{2}{-10}=-\dfrac{1}{5}\)
=>\(\dfrac{x}{y}=-\dfrac{1}{5}\)
=>y=-5x