
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng tslg:
\(\left\{{}\begin{matrix}sinC=\dfrac{AB}{BC}\\cosC=\dfrac{AC}{BC}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AB=sinC.BC=sin30^0.6=3\left(cm\right)\\AC=cosC.BC=cos30^0.6=3\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Áp dụng HTL:
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3.3\sqrt{3}}{6}=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)

2:
A=(x1-x2)^2-x1^2+x1(x1+x2)
=(x1-x2)^2+x1x2
=(x1+x2)^2-3x1x2
=(1/2)^2-3*(-1/4)=1/4+3/4=1

4:
a: cos^2a=1-(1/2)^2=1-1/4=3/4
=>\(cosa=\dfrac{\sqrt{3}}{2}\)
\(tana=\dfrac{1}{2}:\dfrac{\sqrt{3}}{2}=\dfrac{1}{\sqrt{3}}\)
\(cota=1:\dfrac{1}{\sqrt{3}}=\sqrt{3}\)
b: sin^2a=1-(3/4)^2=1-9/16=7/16
=>\(sina=\dfrac{\sqrt{7}}{4}\)
\(tana=\dfrac{\sqrt{7}}{4}:\dfrac{3}{4}=\dfrac{\sqrt{7}}{3}\)
\(cota=1:\dfrac{\sqrt{7}}{3}=\dfrac{3}{\sqrt{7}}\)

b: \(B=\sqrt{\left(2\sqrt{5}-5\right)^2}+\sqrt{29-12\sqrt{5}}\)
\(=\sqrt{\left(5-2\sqrt{5}\right)^2}+\sqrt{\left(2\sqrt{5}-3\right)^2}\)
\(=\left|5-2\sqrt{5}\right|+\left|2\sqrt{5}-3\right|\)
\(=5-2\sqrt{5}+2\sqrt{5}-3=2\)
c: \(C=\dfrac{6}{\sqrt{7}-1}-14\sqrt{\dfrac{1}{7}}+\dfrac{\sqrt{21}+2\sqrt{7}}{2+\sqrt{3}}\)
\(=\dfrac{6\left(\sqrt{7}+1\right)}{7-1}-2\sqrt{7}+\dfrac{\sqrt{7}\left(2+\sqrt{3}\right)}{2+\sqrt{3}}\)
\(=\sqrt{7}+1-2\sqrt{7}+\sqrt{7}=1\)

4A:
a: ΔOBC cân tại O
mà OM là đường cao
nên M là trung điểm của BC
Xét tứ giác OCAB có
M là trung điểm chung của OA và BC
=>OCAB là hình bình hành
mà OB=OC
nên OCAB là hình thoi
b: Xét ΔOAB có OA=OB=AB
nên ΔOAB đều
=>góc BOA=60 độ
=>góc BOE=60 độ
Xét ΔBOE vuông tại B có
tan BOE=BE/BO
=>BE/R=tan60
=>\(BE=R\cdot tan60=R\sqrt{3}\)

\(A=\sqrt{3-\sqrt{5}}-\sqrt{4-\sqrt{15}}+\sqrt{6-3\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\sqrt{6-2\sqrt{5}}-\sqrt{8-2\sqrt{15}}+\sqrt{12-6\sqrt{3}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}-1-\sqrt{5}+\sqrt{3}+3-\sqrt{3}\right)\)
=2/căn 2=căn 2
\(B=\sqrt{4-\sqrt{7}}-\sqrt{14-5\sqrt{3}}-\sqrt{5+\sqrt{21}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8-2\sqrt{7}}-\sqrt{28-10\sqrt{3}}-\sqrt{10+2\sqrt{21}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{7}-1-5+\sqrt{3}-\sqrt{7}-\sqrt{3}\right)\)
=-6/căn 2=-3căn2
\(C=\sqrt{11-6\sqrt{2}}-\sqrt{6-4\sqrt{2}}+\sqrt{7-2\sqrt{6}}\)
=3-căn 2-2+căn 2+căn 6-1
=căn 6
\(D=\sqrt{6-\sqrt{11}}-\sqrt{10+3\sqrt{11}}+2\sqrt{2}-1\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12-2\sqrt{11}}-\sqrt{20+6\sqrt{11}}\right)+2\sqrt{2}-1\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{11}-1-\sqrt{11}-3\right)+2\sqrt{2}-1\)
=-1
\(F=\sqrt{6+3\sqrt{3}}-\sqrt{2+\sqrt{3}}+\sqrt{6-4\sqrt{2}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12+6\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)+2-\sqrt{2}\)
=1/căn 2(3+căn 3-căn 3-1)+2-căn 2
=căn 2+2-căn 2
=2

5.
\(\Delta=\left(-2\right)^2-4\left(-15\right)=64\)
6.
\(\Delta'=2^2-5.\left(-7\right)=39\)
Mà thầy ơi em hok hiểu khúc đầu làm sao để ra cái đó ròi ra kết quả á :((( cả 2 câu lun



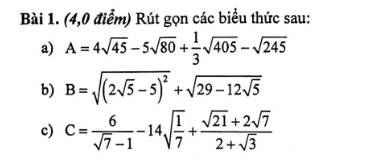





Đề mờ quá. Bạn nên gõ đề ra để mọi người hỗ trợ tốt hơn nhé.