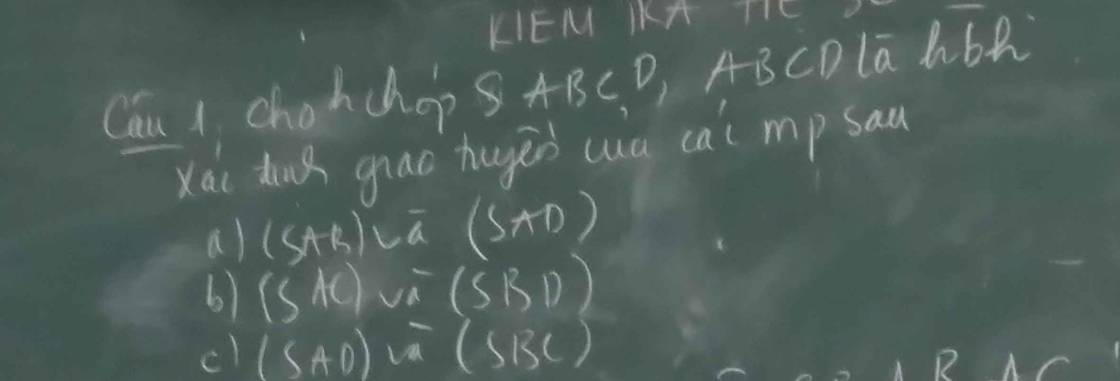 Giúp mình giải bài tập này với các bạn
Giúp mình giải bài tập này với các bạn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




`10)`
Xếp `6` học sinh vào `7` chỗ là `2` lần hoán vị của `6`
`=>` Có `2.6!=1440` cách.
`11)` Chọn `3` học sinh trong `8` học sinh là chỉnh hợp chập `3` của `8`
`=>` Có `A_8 ^3=336` cách.
Xếp 6 học sinh vào 7 chỗ là 2 lần hoán vị của 6
⇒ Có 2.6≠1440 cách.
11) Chọn 33 học sinh trong 88 học sinh là chỉnh hợp chập 33 của 88
⇒ Có \(a\dfrac{3}{8}\)=336 cách.

`\Omega=C_38 ^3`
Gọi `A:`"Chọn `3` học sinh là nam."
`=>A=C_18 ^3`
`=>P(A)=[C_18 ^3]/[C_38 ^3]=68/703`
\(\Omega=c\dfrac{3}{28}\)
gọi a là chọn 3 học sinh là nam
a=\(c\dfrac{3}{18}\)
p(a)=\(\dfrac{c\dfrac{3}{18}}{c\dfrac{3}{38}}\)=\(\dfrac{68}{703}\)

4:
\(n\left(\Omega\right)=C^3_{35}\)
\(n\left(A\right)=C^3_{15}\)
=>\(P\left(A\right)=\dfrac{13}{187}\)

\(\left\{{}\begin{matrix}x=1+t\\y=2+2t\end{matrix}\right.\)
--->vtcp là \(\overrightarrow{u}\)=(1;2)

\(n\left(\Omega\right)=2^3=8\)
Gọi A : '' Nhận 2 mặt sấp ''
\(A=\left\{SNS;SSN;NSS;SSS\right\}\Rightarrow n\left(A\right)=4\)
Xác suất biến cố \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{4}{8}=\dfrac{1}{2}\)


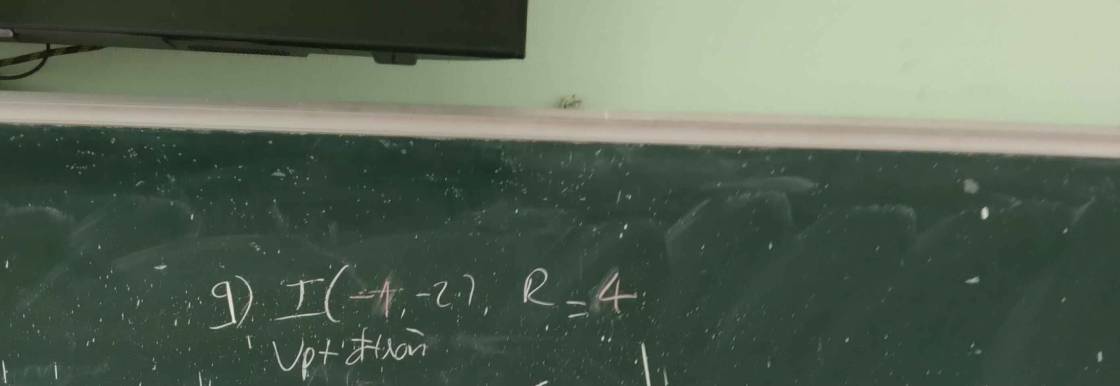
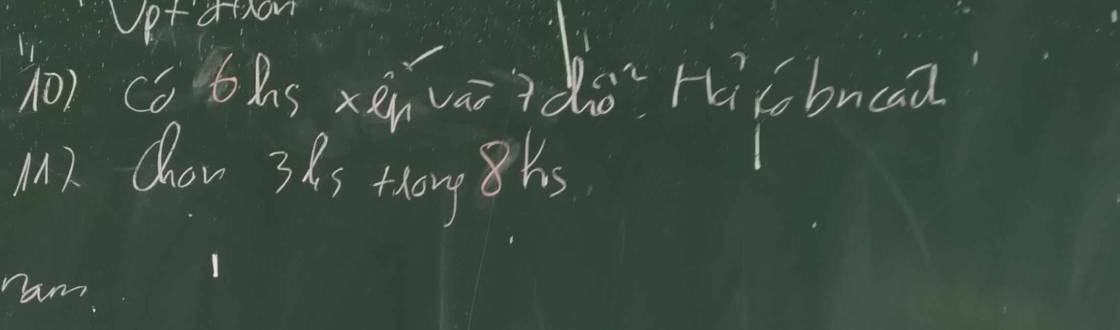
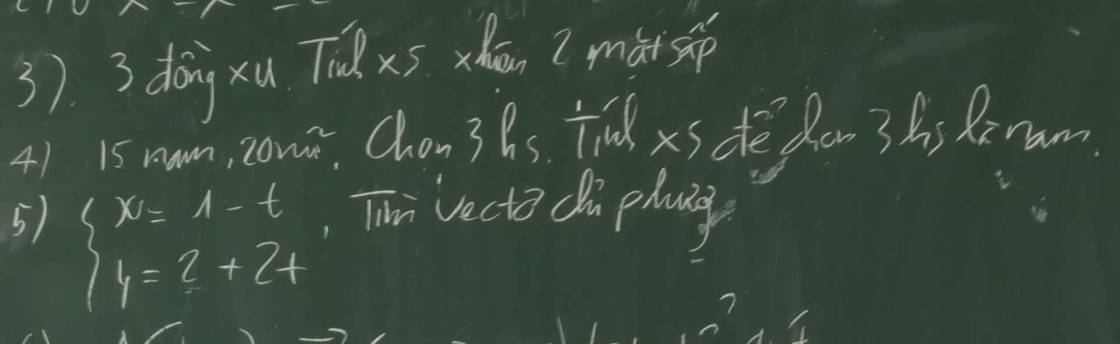


a:
Ta có: \(SA\subset\left(SAB\right)\)
\(SA\subset\left(SAD\right)\)
Do đó: \(\left(SAB\right)\cap\left(SAD\right)=SA\)
b: Gọi O là giao điểm của AC và BD trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
c: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC