\($\hepl{\begin{matrix}u_1=1\\u_{n+1}=2u_n+6\end{matrix}}$\)
Tìm số hạng tổng quát của dãy số sau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HN
Hồng Nhan
17 tháng 11 2023
Đúng(0)
Những câu hỏi liên quan
30 tháng 8 2021
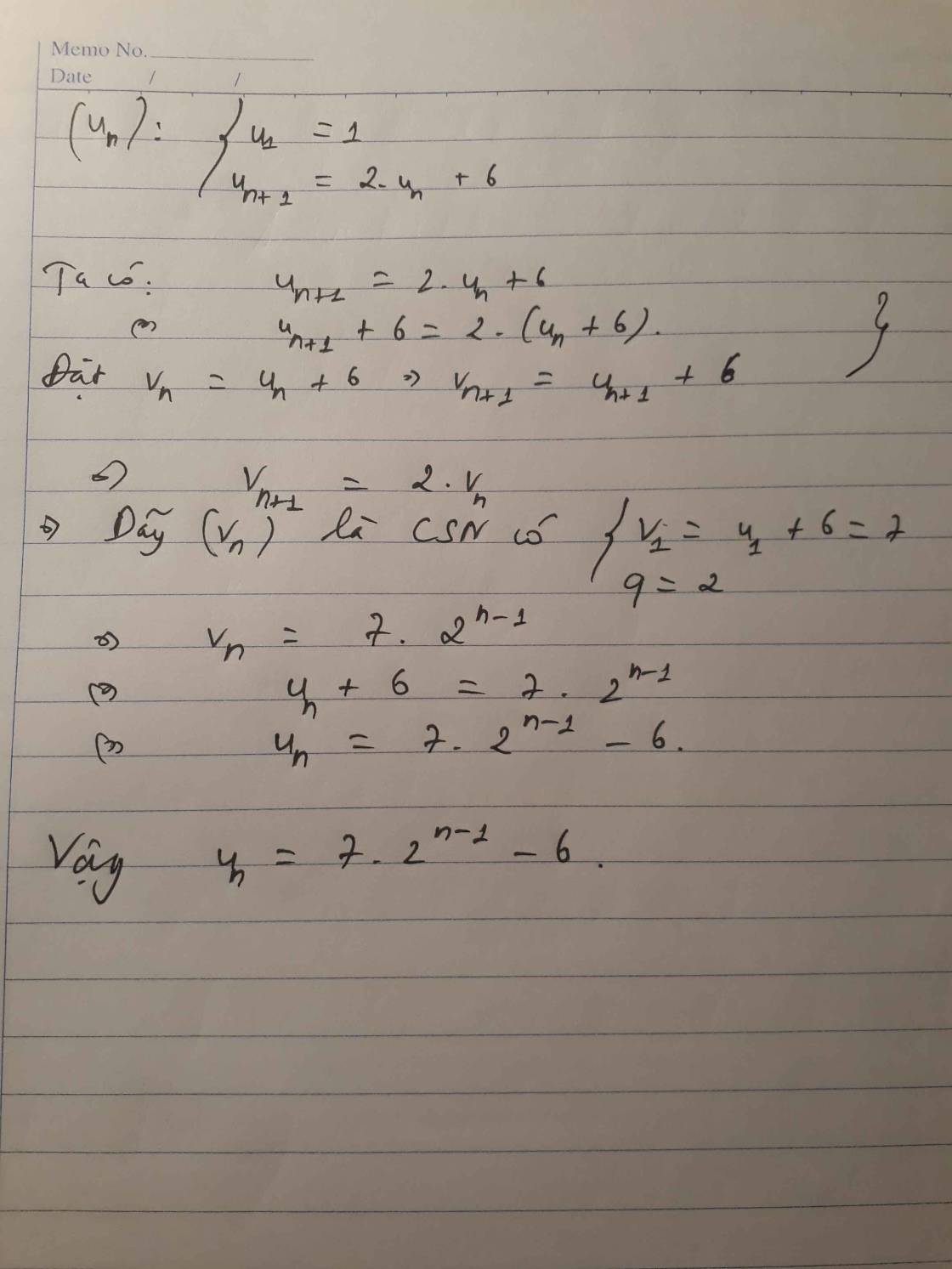
Dự đoán : số hạng tổng quát là un = 2n (lại bảo sai đi :)) số trước nhân với 2 thì được số sau, chả là lũy thừa chứ còn gì 
)
+ Với n = 1 thì u1 = 1 : đúng
+ Giả sử điều dự đoán đúng với n = k ≥ 1
⇒ uk = 2k
⇒ 2uk = 2k . 2 = 2k+1
Mặt khác : 2uk = uk+1 (theo công thức truy hồi)
⇒ uk+1 = 2k+1
Vậy điều dự đoán đúng với n = k + 1
Mà ta có : điều này đúng với n = 1 , nên sẽ đúng với n = 2, rồi n = 3 , n = 4 .... Vậy là đúng với mọi x là số nguyên dương
Đáp án : un = 2n
15 tháng 10 2023
1:
a: \(u_2=2\cdot1+3=5;u_3=2\cdot5+3=13;u_4=2\cdot13+3=29;\)
\(u_5=2\cdot29+3=61\)
b: \(u_2=u_1+2^2\)
\(u_3=u_2+2^3\)
\(u_4=u_3+2^4\)
\(u_5=u_4+2^5\)
Do đó: \(u_n=u_{n-1}+2^n\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2021
\(u_{n+1}=\dfrac{2u_n}{u_n+4}\Leftrightarrow\dfrac{1}{u_{n+1}}=\dfrac{1}{2}+\dfrac{2}{u_n}\)
Đặt \(v_n=\dfrac{1}{u_n}\Rightarrow\left\{{}\begin{matrix}v_1=1\\v_{n+1}=2v_n+\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}v_1=1\\v_{n+1}+\dfrac{1}{2}=2\left(v_n+\dfrac{1}{2}\right)\end{matrix}\right.\)
Đặt \(v_n+\dfrac{1}{2}=x_n\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{3}{2}\\x_{n+1}=2x_n\end{matrix}\right.\)
\(\Rightarrow x_n\) là CSN với công bội 2 \(\Rightarrow x_n=\dfrac{3}{2}.2^{n-1}=3.2^{n-2}\)
\(\Leftrightarrow v_n=x_n-\dfrac{1}{2}=3.2^{n-2}-\dfrac{1}{2}\)
\(\Rightarrow u_n=\dfrac{1}{v_n}=\dfrac{1}{3.2^{n-2}-\dfrac{1}{2}}=\dfrac{2}{3.2^{n-1}-1}\)