 giúp em với trc tối nay ạ
giúp em với trc tối nay ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(2^4.5-\left[31-9^2\right]=16.5-\left(31-81\right)=80-\left(-50\right)=130\)
\(2^4\).5-[1.31-(13-4)^2]
=16.5-[1.31-81]
=16.5-[31-81]
=16.5-(-50)
=80-(-50)
=130

a: \(9x^2+12x+4=\left(3x+2\right)^2\)
b: \(x^2-10x+25=\left(x-5\right)^2\)
c: \(4x^2+4x+1=\left(2x+1\right)^2\)
d: \(x^2+x+\dfrac{1}{4}=\left(x+\dfrac{1}{2}\right)^2\)
e: \(x^2-x+\dfrac{1}{4}=\left(x-\dfrac{1}{2}\right)^2\)
f: \(4x^2y^4-12xy^2+9=\left(2xy^2-3\right)^2\)
g: \(16x^2+24x+9=\left(4x+3\right)^2\)
h: \(\dfrac{x^2}{4}-3x+9=\left(\dfrac{1}{2}x-3\right)^2\)
i: \(\dfrac{25}{x^2}-\dfrac{10}{x}+1=\left(\dfrac{5}{x}-1\right)^2\)
a) \(9x^2+12x+4=\left(3x+2\right)^2\)
b) \(x^2+25-10x=\left(x-5\right)^2\)
c) \(4x^2+4x+1=\left(2x+1\right)^2\)
d) \(x^2+x+\dfrac{1}{4}=\left(x+\dfrac{1}{2}\right)^2\)
e) \(x^2-x+\dfrac{1}{4}=\left(x-\dfrac{1}{2}\right)^2\)
f) \(4x^2y^4-12xy^2+9=\left(2xy^2-3\right)^2\)
g) \(16x^2+24x+9=\left(4x+3\right)^2\)
h) \(\dfrac{x^2}{4}-3x+9=\left(\dfrac{x}{2}-3\right)^2\)
i) \(\dfrac{25}{x^2}-\dfrac{10}{x}+1=\left(\dfrac{5}{x}-1\right)^2\)

6:
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2

3: Ta có: \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-1\right)\left(x+1\right)=27\)
\(\Leftrightarrow x^3-27-x^3+x=27\)
hay x=54

a.b.\(n_P=\dfrac{m_P}{M_P}=\dfrac{6,2}{31}=0,2mol\)
\(n_{O_2}=\dfrac{V_{O_2}}{22,4}=\dfrac{6,72}{22,4}=0,3mol\)
\(4P+5O_2\rightarrow\left(t^o\right)2P_2O_5\)
0,2 < 0,3 ( mol )
0,2 0,25 0,1 ( mol )
Chất còn dư là O2
\(V_{O_2\left(dư\right)}=n_{O_2\left(dư\right)}.22,4=\left(0,3-0,25\right).22,4=1,12l\)
\(m_{P_2O_5}=n_{P_2O_5}.M_{P_2O_5}=0,1.142=14,2g\)
c.\(2KClO_3\rightarrow\left(t^o,MnO_2\right)2KCl+3O_2\)
1/6 0,25 ( mol )
\(m_{KClO_3}=n_{KClO_3}.M_{KClO_3}=\dfrac{1}{6}.122,5=20,41g\)
a) PTHH: \(4P+5O_2\rightarrow^{t^0}2P_2O_5\)
b) \(n_P=\dfrac{m}{M}=\dfrac{6,2}{31}=0,2\left(mol\right);n_{O_2}=\dfrac{V}{22,4}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\)
\(4P+5O_2\rightarrow^{t^0}2P_2O_5\)
4 : 5 : 2
0,2 : 0,3
-So sánh tỉ lệ: \(\dfrac{0,2}{4}< \dfrac{0,3}{5}\)
\(\Rightarrow\)P phản ứng hết còn O2 dư.
\(m_{O_2\left(dư\right)}=16.0,3-16.\dfrac{0,2.5}{4}=0,8\left(g\right)\)
c) -Theo PTHH trên:
\(n_{P_2O_5}=\dfrac{0,2.2}{4}=0,1\left(mol\right)\)
\(\Rightarrow m_{P_2O_5}=n.M=142.0,1=14,2\left(g\right)\)
d) -Theo PTHH trên:
\(n_{O_2\left(LT\right)}=\dfrac{0,2.5}{4}=0,25\left(mol\right)\)
PTHH: \(2KClO_3\rightarrow^{t^0}2KCl+3O_2\uparrow\)
2 : 2 : 3
\(\dfrac{1}{6}\) : \(\dfrac{1}{6}\) : 0,25
\(\Rightarrow m_{KClO_3}=n.M=\dfrac{1}{6}.122,5=\dfrac{245}{12}\left(g\right)\)

12:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: Xét ΔNAC và ΔNBE có
góc NAC=góc NBE
NA=NB
góc ANC=góc BNE
=>ΔNAC=ΔNBE
=>AC=BE
c: Xét tứ giác AEBC có
AC//BE
AC=BE
=>AEBC là hình bình hành
=>AE//BC
d: Xét ΔEAC có EF/EA=EN/EC
nên FN//AC//EB
Xét ΔECB có CM/CB=CN/CE
nên NM//EB
=>F,N,M thẳng hàng
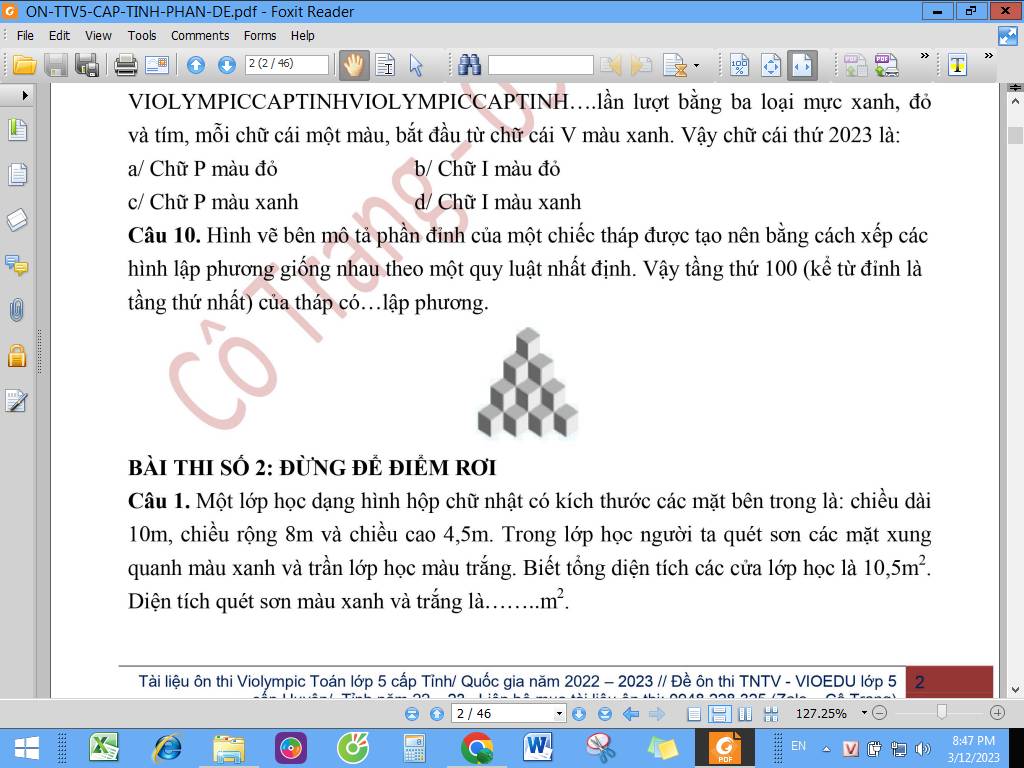
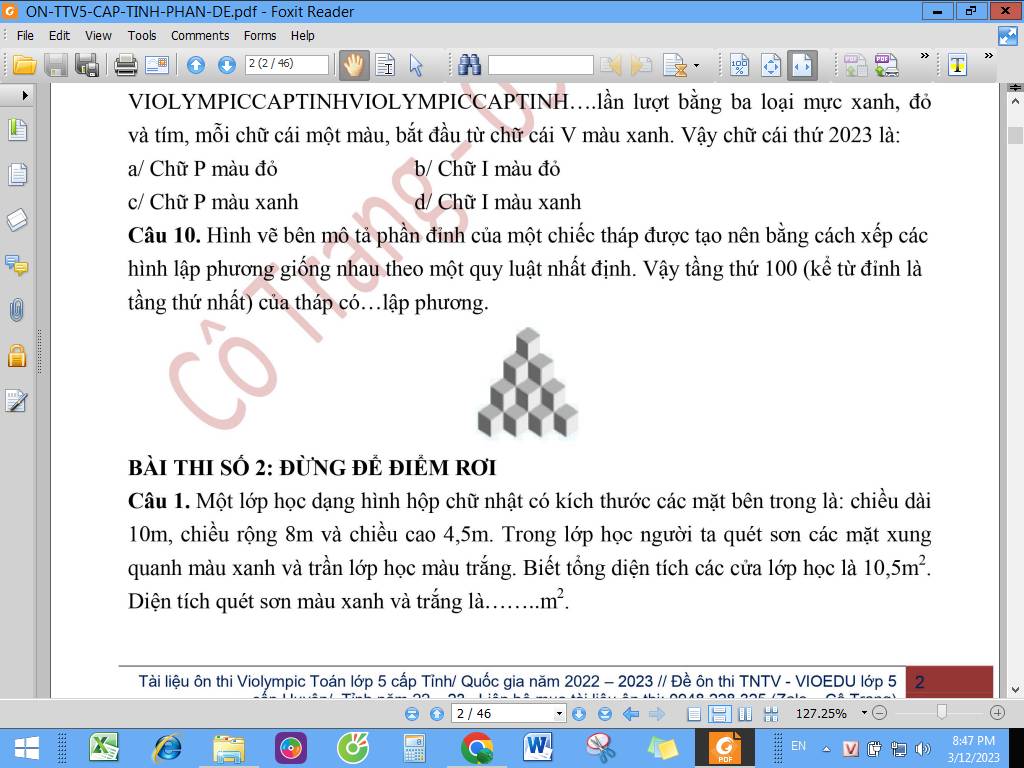
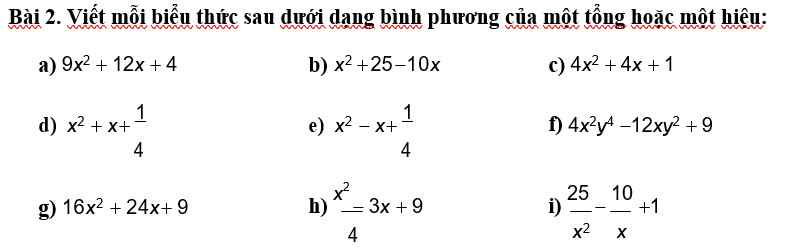 giúp em với ạ em cần gấp trong tối nay
giúp em với ạ em cần gấp trong tối nay  giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ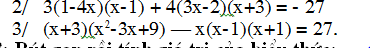

 * Mọi người cố giúp em hoàn thiện trong buổi tối nay với ạ, em đg cần gấp! Cảm ơn ạ!
* Mọi người cố giúp em hoàn thiện trong buổi tối nay với ạ, em đg cần gấp! Cảm ơn ạ!
Bài 1:
1. $2^n+2^{n+3}=144$
$2^n(1+2^3)=144$
$2^n.9=144$
$2^n=144:9=16=2^4\Rightarrow n=4$
2.
$3^n+3^{n+2}=270$
$3^n(1+3^2)=270$
$3^n.10=270$
$3^n=270:10=27=3^3\Rightarrow n=3$
3.
$2^n+2^{n+1}+2^{n+2}+2^{n+3}=960$
$2^n(1+2+2^2+2^3)=960$
$2^n.15=960$
$2^n=960:15=64=2^6$
$\Rightarrow n=6$
4.
$3^n+3^{n+1}+3^{n+2}+3^{n+3}=3240$
$3^n(1+3+3^2+3^3)=3240$
$3^n.40=3240$
$3^n=3240:40=81=3^4\Rightarrow n=4$
Bài 2:
1. $(x+1)^2=49=7^2$
$\Rightarrow x+1=7$
$\Rightarrow x=6$
2.
$(x+2)^3=512=8^3$
$\Rightarrow x+2=8\Rightarrow x=6$
3.
$(x-3)^9=(x-3)$
$\Rightarrow (x-3)^9-(x-3)=0$
$\Rightarrow (x-3)[(x-3)^8-1]=0$
$\Rightarrow x-3=0$ hoặc $(x-3)^8-1=0$
$\Rightarrow x-3=0$ hoặc $(x-3)^8=1=1^8=(-1)^8$
$\Rightarrow x=3$ hoặc $x-3=1$ hoặc $x-3=-1$
$\Rightarrow x=3$ hoặc $x=4$ hoặc $x=2$