Tìm x,y biết: x2 + 2x + y2 + 6y + 10=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, (x^2 -2x+1)+(y^2 +6y+9) =0
(x-1)^2 +(y+3)^2 =0
Do đó: x-1=0 và y+3=0
Vậy x=1 và y=-3
b, x^2 +y^2 +1=xy+x+y
2x^2 +2y^2 +2=2xy+2x+2y
2x^2 +2y^2 -2xy-2x-2y +2=0
(x^2 -2x+1)+(y^2 -2y+1)+ (x^2 +y^2 -2xy)=0
(x-1)^2 +(y-1)^2 +(x-y)^2 =0
Suy ra: x-1=0, y-1=0 và x-y=0
Vậy x=1,y=1
c,5x^2 - 4x-2xy+y^2 +1=0
(4x^2 -4x+1)+(x^2 -2xy+y^2 )=0
(2x-1)^2 +(x-y)^2 =0
Do đó: 2x-1 =0 và x=y suy ra: x=0,5 và x=y
Vậy x=y=0,5

+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.

\(a,9x^2+y^2+2z^2-18x+4z-6y+20=0\\ \Leftrightarrow9\left(x-1\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\\z=-1\end{matrix}\right.\)
\(b,5x^2+5y^2+8xy+2y-2x+2=0\\ \Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-y\\x=1\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(c,5x^2+2y^2+4xy-2x+4y+5=0\\ \Leftrightarrow\left(2x+y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x=-y\\x=1\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(d,x^2+4y^2+z^2=2x+12y-4z-14\\ \Leftrightarrow\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3}{2}\\z=-2\end{matrix}\right.\)
\(e,x^2+y^2-6x+4y+2=0\\ \Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
Pt vô nghiệm do ko có 2 bình phương số nguyên có tổng là 11
e: Ta có: \(x^2-6x+y^2+4y+2=0\)
\(\Leftrightarrow x^2-6x+9+y^2+4y+4-11=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
Dấu '=' xảy ra khi x=3 và y=-2

a.
\(1-4x^2=\left(1-2x\right)\left(1+2x\right)\)
b.
\(8-27x^3=\left(2\right)^3-\left(3x\right)^3=\left(2-3x\right)\left(4+6x+9x^2\right)\)
c.
\(27+27x+9x^2+x^3=x^3+3.x^2.3+3.3^2.x+3^3\)
\(=\left(x+3\right)^3\)
d.
\(2x^3+4x^2+2x=2x\left(x^2+2x+1\right)=2x\left(x+1\right)^2\)
e.
\(x^2-y^2-5x+5y=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-5\right)\)
f.
\(x^2-6x+9-y^2=\left(x-3\right)^2-y^2=\left(x-3-y\right)\left(x-3+y\right)\)

Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính 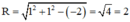
b) 16x2 + 16y2 + 16x – 8y –11 = 0
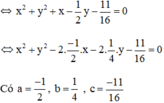
⇒ Đường tròn có tâm 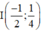 , bán kính
, bán kính 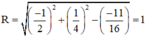
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính 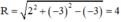
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
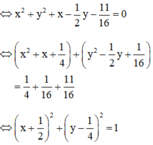
Vậy đường tròn có tâm 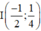 và bán kính R = 1.
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.

c)Ta có: x2 + y2 – 2x + 4y + 5 = (x2 – 2x + 1) + (y2 + 4y + 4)
= (x – 1)2 + (y + 2)2
Vậy (x – 1)2 + (y + 2)2 = 0 ⇒ x – 1 = 0 hay y + 2 = 0
⇒ x = 1 hoặc y = -2

\(a,\Leftrightarrow\left(9x^2-18x+9\right)+\left(y^2-6y+9\right)+\left(2z^2+4z+2\right)=0\\ \Leftrightarrow9\left(x-1\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\\z=-1\end{matrix}\right.\)
\(b,\Leftrightarrow\left(4x^2+8xy+4y^2\right)+\left(x^2-2x+1\right)+\left(y^2+2y+1\right)=0\\ \Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-y\\x=1\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(c,\Leftrightarrow\left(4x^2+4xy+y^2\right)+\left(x^2-2x+1\right)+\left(y^2+4y+4\right)=0\\ \Leftrightarrow\left(2x+y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x=-y\\x=1\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
a,9x^2+y^2+2z^2−18x+4z−6y+20=0
⇔9(x−1)^2+(y−3)^2+2(z+1)^2=0
⇔x=1;y=3;z=−1
b,5x^2+5y^2+8xy+2y−2x+2=0
⇔4(x+y)2+(x−1)2+(y+1)2=0
⇔x=−y;x=1y=−1⇔x=1y=−1
c,5x^2+2y^2+4xy−2x+4y+5=0
⇔(2x+y)^2+(x−1)^2+(y+2)^2=0
⇔2x=−y;x=1;y=−2
⇔x=1;y=−2
d,x^2+4y^2+z^2=2x+12y−4z−14
⇔(x−1)^2+(2y−3)^2+(z+2)^2=0
⇔x=1;y=3/2;z=−2
e: Ta có: x^2−6x+y2+4y+2=0
⇔x^2−6x+9+y^2+4y+4−11=0
⇔(x−3)^2+(y+2)^2=11
Dấu '=' xảy ra khi x=3 và y=-2

\(a,P=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
Dấu \("="\Leftrightarrow x=1\)
\(b,Q=2x^2-6x=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{9}{4}\right)=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(c,M=\left(x^2-x+\dfrac{1}{4}\right)+\left(y^2+6y+9\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-3\end{matrix}\right.\)
a: Ta có: \(P=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1

a) \(P=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\)
\(MinP=4\Leftrightarrow x-1=0\Rightarrow x=1\)
b) \(Q=2x^2-6x\)
\(=2\left(x^2-3x\right)\)
\(=2\left(x^2-2.x.\frac{3}{2}+\frac{9}{4}-\frac{9}{4}\right)\)
\(=2\left(\left(x-\frac{3}{2}\right)^2-\frac{9}{4}\right)\)
\(=-\frac{9}{2}-2\left(x-\frac{3}{2}\right)^2\le\frac{-9}{2}\)
\(MinQ=\frac{-9}{2}\Leftrightarrow x-\frac{3}{2}=0\Rightarrow x=\frac{3}{2}\)
M=x^2+y^2-x+6y+10
M=(x^2-x+1/4)+(y^2+6y+9)+3/4
M=(x-1/2)^2+(y+3)^2+3/4
\(minM=\frac{3}{4}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=-3\end{cases}}\)
\(\Leftrightarrow x^2+2x+1+y^2+6y+9=0\)
\(\Leftrightarrow\left(x+1\right)^2+\left(y+3\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)^2=0\\\left(y+3\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-1\\y=-3\end{cases}}}\)
vậy \(x=-1;y=-3\)