Tìm GTNN của biểu thức M = x2 - 2x(y+1) + 3y2 + 2025
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KR
7 tháng 5 2018
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
HN
2
H9
HT.Phong (9A5)
CTVHS
27 tháng 7 2023
Ta có:
\(2x+y=11z\) và \(3x-y=4z\)
Chia theo vế ta có:
\(\dfrac{2x+y}{3x-y}=\dfrac{11z}{4z}=\dfrac{11}{4}\)
\(\Leftrightarrow4\left(2x+y\right)=11\left(3x-y\right)\)
\(\Leftrightarrow8x+4y=33x-11y\)
\(\Leftrightarrow15y=25x\)
\(\Leftrightarrow3y=5x\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{5}=k\)
\(\Rightarrow x=3k,y=5k\)
Thay vào Q ta có:
\(Q=\dfrac{2\cdot\left(3k\right)^2-3\cdot3k\cdot5k}{\left(3k\right)^2+3\cdot\left(5y\right)^2}\)
\(Q=\dfrac{18k^2-45k^2}{9k^2+75k^2}\)
\(Q=\dfrac{k^2\left(18-45\right)}{k^2\left(9+75\right)}\)
\(Q=\dfrac{-27}{84}=-\dfrac{9}{28}\)
27 tháng 7 2023
\(\dfrac{2x+y}{3x-y}=\dfrac{11}{4}\)
=>33x-11y=8x+4y
=>25x=15y
=>5x=3y
=>x/3=y/5=k
=>x=3k; y=5k
\(Q=\dfrac{2\cdot9k^2-3\cdot3k\cdot5k}{9k^2+3\cdot25k^2}=\dfrac{18-9\cdot5}{9+3\cdot25}=\dfrac{-9}{28}\)
13 tháng 1 2023
3x^2+3y^2+4xy-2x+2y+2=0
=>2x^2+4xy+2y^2+x^2-2x+1+y^2+2y+1=0
=>x=1 và y=-1
M=(1-1)^2017+(1-2)^2018+(-1+1)^2015=1
31 tháng 8 2018
bài 4 : ta có : \(x+2y=3\Leftrightarrow x=3-2y\)
\(\Rightarrow E=x^2+2y^2=\left(3-2y\right)^2+2y^2=4y^2-12y+9+2y^2\)
\(=6y^2-12y+6+3=6\left(y-1\right)^2+3\ge3\)
\(\Rightarrow E_{max}=3\) khi \(x=y=1\)
bài 5 : ta có : \(x^2+3y^2+2xy-10x-14y+18=0\)
\(\Leftrightarrow2y^2-4y+2=-\left(x^2+2xy+y^2\right)+10\left(x+y\right)-16\)
\(\Leftrightarrow2\left(y-1\right)^2=-\left(x+y\right)^2+10\left(x+y\right)-16\ge0\)
\(\Leftrightarrow2\le x+y\le8\)
\(\Rightarrow P_{min}=2\) khi \(\left\{{}\begin{matrix}y=1\\x+y=2\end{matrix}\right.\Leftrightarrow x=y=1\)
\(\Rightarrow P_{max}=8\) khi \(\left\{{}\begin{matrix}y=1\\x+y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=1\end{matrix}\right.\)
vậy ...........................................................................................................................
CM
3 tháng 11 2018
Ta có
M = 3 x 2 ( x 2 + y 2 ) + 3 y 2 ( x 2 + y 2 ) – 5 ( y 2 + x 2 ) = ( x 2 + y 2 ) ( 3 x 2 + 3 y 2 – 5 ) = ( x 2 + y 2 ) [ 3 ( x 2 + y 2 ) – 5 ]
Mà x 2 + y 2 = 1 nên M = 1.(3.1 – 5) = -2. Vậy M = -2
Đáp án cần chọn là: D
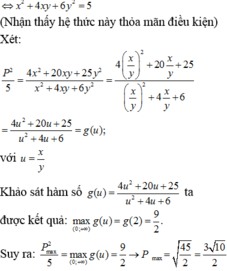
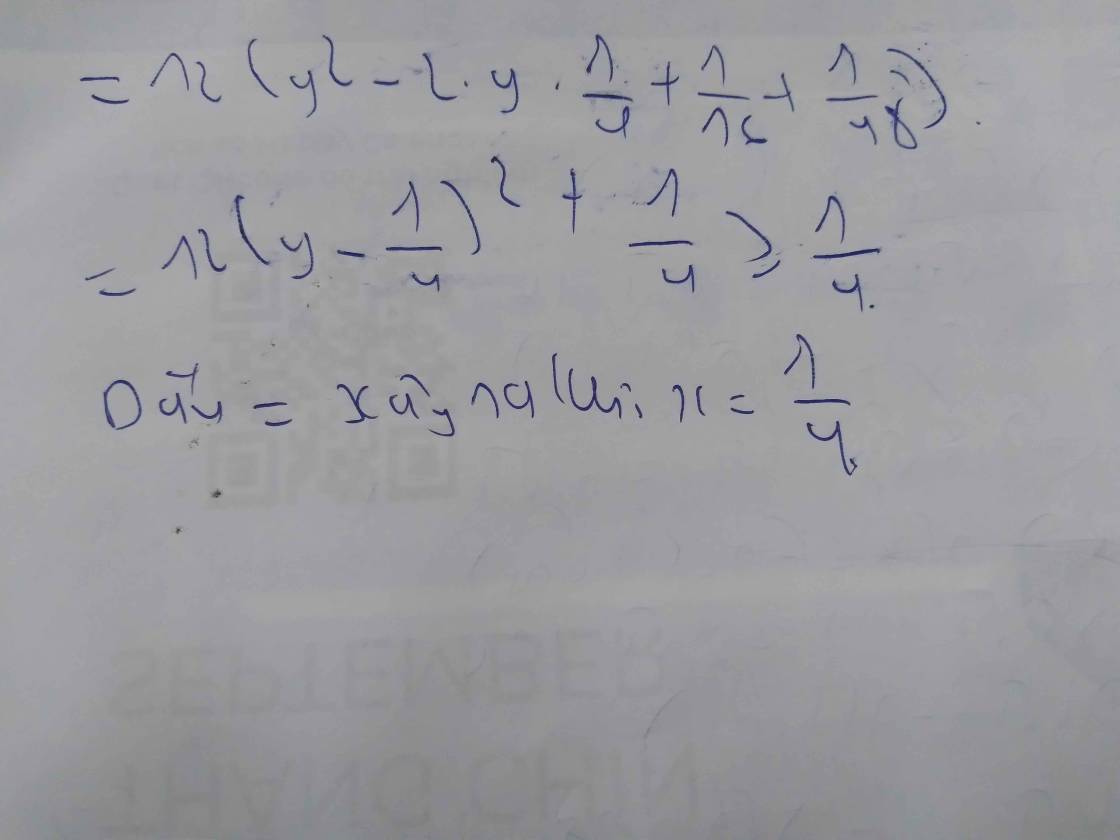
Ta có:
\(M=x^2-2x\left(y+1\right)+3y^2+2025\)
\(M=x^2-2\cdot x\cdot\left(y+1\right)+\left(y+1\right)^2+3y^2+2025-\left(y+1\right)^2\)
\(M=\left[x-\left(y+1\right)\right]^2+3y^2+2025-y^2-2y-1\)
\(M=\left(x-y-1\right)^2+2y^2-2y+2024\)
\(M=\left(x-y-1\right)^2+2\left(y-\dfrac{1}{2}\right)^2+\dfrac{4047}{2}\)
Mà: \(\left\{{}\begin{matrix}\left(x-y-1\right)^2\ge0\\2\left(y-\dfrac{1}{2}\right)^2\ge0\end{matrix}\right.\)
\(\Rightarrow M=\left(x-y-1\right)^2+2\left(y-\dfrac{1}{2}\right)^2+\dfrac{4047}{2}\ge\dfrac{4047}{2}\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}x-y-1=0\\y-\dfrac{1}{2}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}+1\\y=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy GTNN của M là ....