Kết quả thí nghiệm đo được trong một lần thí nghiệm với hai xe có cùng khối lượng là 245 g, xe 1 có tốc độ 0,542 m/s va chạm với xe 2 đang đứng yên, sau va chạm đo được hai xe có cùng tốc độ là 0,269 m/s. Hãy tính động lượng của từng xe trước và sau va chạm, từ đó so sánh động lượng của hệ hai xe trước và sau va chạm. Định luật bảo toàn có được nghiệm đúng hay không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn chiều dương là chiều chuyển động của hai xe
Áp dụng công thức v = v 0 + a t ⇒ a = v − v 0 t
Đối với xe một: a 1 = v 1 − v 01 t = 100 − 50 t = 50 t
Đối với xe hai: a 2 = v 2 − v 02 t = 100 − 150 t = − 50 t
Hai xe va chạm nhau theo định luật III Newton ta có
F 12 = − F 21 ⇒ m 2 a 2 = − m 1 a 1 ⇒ m 2 ( − 50 t ) = − m 1 50 t ⇒ m 1 = m 2

Chọn đáp án D
? Lời giải:
+ Chọn chiều dương là chiều chuyển động của hai xe
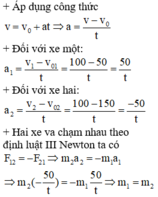

Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)V\)
\(\Rightarrow3000\cdot4+2000\cdot2=\left(3000+2000\right)\cdot V\)
\(\Rightarrow V=3,2\)m/s

Chọn chiều dương là chiều chuyển động toa thứ nhất
Áp dụng định luật bảo toàn động lương:
\(mv=m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}\)
\(\Rightarrow mv=m_1v_1-m_2v_2\)
\(\Rightarrow5v=3.6-2.4\) => v = 2 m/s

Áp dụng định luật bảo toàn động lượng , ta có :
\(\overrightarrow{p_t}=\overrightarrow{p_s}\Rightarrow m_vv1=\overrightarrow{m_{1v'_1}}+\overrightarrow{m_{2v_2}}\)
Chiều dương là chiều chuyển động ban đầu của xe 1 :
\(\Rightarrow3.4=2,5.m_2+0,5\)
\(\Rightarrow12-0,5=2,5.m_2\)
\(\Rightarrow11,5:2,5=m_2\)
Vậy khối lượng toa 2 là :
\(11,5:2,5=4,6\left(tấn\right)\)

Do sau khi va chạm 2 xe dính vào nhau và chuyển động với một vận tốc ⇒ Đây là va chạm mềm
Chọn chiều dương là chuyển động của 2 vật:
Đặt \(\upsilon_1,\upsilon_2,\upsilon_3\) lần lược và vận tốc của xe A, xe B và của 2 xe sau khi va chạm, nên ta có:
\(m_1\upsilon_1+m_2\upsilon_2=\left(m_1+m_2\right).\upsilon_3\)
\(\Rightarrow\upsilon_3=\dfrac{m_1\upsilon_1+m_2\upsilon_2}{m_1+m_2}=\dfrac{2.5+1.0}{2+1}\approx3,67m/s\)

Theo định luật bảo toàn cơ năng:
\(m_1v_1+m_2v_2=m_1v_1'+m_2v_2'\)
\(\Rightarrow m_1\cdot50+m_2\cdot100=m_1\cdot100+m_2\cdot100\)
\(\Rightarrow m_1=m_2\)
\(\Rightarrow\dfrac{m_1}{m_2}=1\)
Động lượng của các xe trước va chạm:
+ Xe 1: \({p_1} = {m_1}.{v_1} = 0,245.0,542 \approx 0,133(kg.m/s)\)
+ Xe 2: \({p_2} = {m_2}.{v_2} = 0\)(do xe 2 đứng yên nên v2 = 0)
=> Động lượng của hệ trước va chạm là: p = 0,133 kg.m/s
Động lượng của các xe sau va chạm
+ Xe 1: \(p_1' = {m_1}.v_1' = 0,245.0,269 \approx 0,066(kg.m/s)\)
+ Xe 2: \(p_2' = {m_2}.v_2' = 0,245.0,269 \approx 0,066(kg.m/s)\)
=> Động lượng của hệ sau va chạm là: p’ = 0,132 kg.m/s
=> Động lượng của hệ trước và sau va chạm gần như bằng nhau
=> Định luật bảo toàn động lượng được nghiệm đúng.