Hình vuông ABCD có cạnh 12cm.Trên đoạn BD lấy điểm E,F sao cho BE=EF=FD.Tính diện tích AECF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 8 2021
Ta có 3 tam giác ADF ; AFE ; AEB có chung chiều cao hạ từ đỉnh A xuống DB, có đáy DF = FE = EB => SADF = SCEB
\(\Rightarrow S^{AFE}=\frac{1}{3}S^{ADB}\)
Ta thấy 3 tam giác CDF ; FCE ; CEB có chung chiều cao hạ từ đỉnh C xuống DB, có đáy : DF = FE = EB => SCDF = SFCE = SCEB
\(\Rightarrow S^{FCE}=\frac{1}{3}S^{DCB}\)
\(\Rightarrow S^{AECF}=S^{AFE\:}+S^{FCE}\)
\(=\frac{1}{3}S^{ADB}+\frac{1}{3}S^{CDB}\)
\(=\frac{1}{3}\left(S^{ADB}+S^{CDB}\right)=\frac{1}{3}S^{ABCD}\)
\(=\frac{1}{3}\times\left(12\times12\right)=\frac{1}{3}\times144=48\left(cm^2\right)\)
Vậy SAECF là 48cm2
6 tháng 8 2017
Diện tích hình vuông ABCD là:
12 x 12 = 144 (cm2)
Diện tích hình tam giác ABD hay Diện tích hình tam giác BDC là:
144 : 2 = 72 (cm2)
So sánh: SCEF và SBDC
SCEF = 1/3 SBDC vì:
- Đáy FE = 1/3 đáy BD
- Chung chiều cao hạ từ C xuống BD
Diện tích hình tam tam giác CEF là:
72 x 1/3 =24 (cm2)
SAFE = 1/3 SABD vì:
- đáy FE = 1/3 đáy BD
- Chung chiều cao hạ từ A xuống BD
Diện tích hình tam giác ABD là:
72 x 1/3 = 24 (cm2)
Diện tích hình AECF là:
24 + 24 = 48 (cm2)
Đáp số: 48 cm2
DD
6 tháng 8 2017
Xét 3 tam giác ADF; AFE và AEB có: chung chiều cao hạ từ đỉnh A xuống DB; có đáy DF = FE = EB
=> Diện tích ADF= Diện tích FAE= Diện tích AEB
=> Diện tích FAE=1/3 x Diện tích ADB
Xét 3 tam giác CDF ; FCE; CEB có: chung chiều cao hạ từ đỉnh C xuống BD; đáy DF = đáy FE = đáy EB
=> Diện tích DFE= Diện tích FCE= Diện tích CEB
=> Diện tích FCE= 1/3 x Diện tích DCB
Ta có: Diện tích AECF= Diện tích FAE+ Diện tích FCE = 1/3x Diện tích ADB + 1/3 Diện tích DCB= 1/3x (Diện tích ADB+ Diện tích DCB) = 1/3 x Diện tích ABCD= 1/3 x 12x12 = 48cm vuông
đáp án: 48cm vuông
Bạn có viết tắt chữ Diện tích bằng chữ S được nhé
21 tháng 8 2021
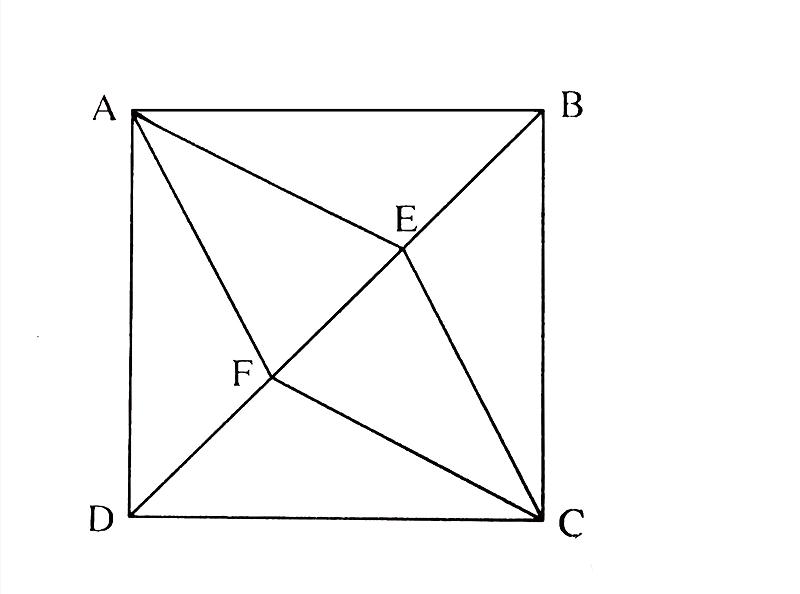
Ta có: △ ADF ; △ AFE ; △ AEB có chung chiều cao, hạ từ đỉnh A xuống DB, có đáy DF = FE = EB ⇒ \(S_{ADF}=S_{AFE}=S_{AEB}\)
⇒ \(S_{AFE}=\dfrac{1}{3}S_{ADB}\)
Ta lại có: △ CDF ; △ FCE ; △ CEB có chung chiều cao, hạ từ đỉnh C xuống DB, có đáy DF = FE = EB ⇒ \(S_{CDF}=S_{FCE}=S_{CEB}\)
⇒ \(S_{FCE}=\dfrac{1}{3}S_{DCB}\)
Vậy \(S_{AECF}=S_{AFE}+S_{FCE}=\dfrac{1}{3}S_{ADB}+\dfrac{1}{3}S_{DCB}\) \(=\dfrac{1}{3}\left(S_{ADB}+S_{DCB}\right)=\dfrac{1}{3}S_{AECF}=\dfrac{1}{3}\times\left(12\times12\right)=48\left(cm^2\right)\)
1 tháng 1 2016
Xét ba tam giác ADF,AFE,AEB có:chung chiều cao hạ từ đỉnh A xuống DB có đáy DF=FE=EB
=>SADF=SFAE=SAEB
=>SFAE=1/3 x SADB
Xét 3 tam giác CDF,FCE,CEB có chung chiều cao hạ từ đỉnh C xuống BD đáy DF=FE=EB
=>SDFE=SFCE=SCEB
=>SFCE=1/3 x SDCB
Ta có: SAECF=SFAE+SFCE=1/3x SADB+1/3 x SDCB=1/3x(SADB+SDCB)=1/3 x SABCD=1/3 x12 x12=48 (cm2)
Tick cho mình nha Đỗ Vân Nhi
4 tháng 2 2016
Mình không biết vẽ hình trên OnlineMath
S AECF là ;
12x12:3=48 (cm2)
Đáp số : 48cm2
NM
Hình vuông ABCD có cạnh 12cm. Trên đoạn BD lấy điểm Evà F sao cho BE=EF=FD.Tính diện tích hình AECF?
0
23 tháng 4 2021
Đáp án:Ta có:BE=EF=FD=BD:3=12:3=4(cm)
Diện tích ABE là:BExAB:2
Diện tích CDF là:FDxCD:2 Mà BE=FD=4cm;AB=CD=12cm
=>Diện tích ABE=Diện tích CDF=4x12:2=24(cm2)
Diện tích hình vuông ABCD là:
12x12=144(cm2)
Diện tích AECF là:
144-24x2=144-48=96(cm2)
Đáp số: 96(cm2)
S
20 tháng 2 2018
Cho hình vuông ABCD có cạnh 12 cm. Trên đoạn BD lấy điểm E,F sao cho BE=EF=FD. Tính diện tích tứ giác AECFCho hình vuông ABCD có cạnh 12 cm. Trên đoạn BD lấy điểm E,F sao cho BE=EF=FD. Tính diện tích tứ giác AECFCho hình vuông ABCD có cạnh 12 cm. Trên đoạn BD lấy điểm E,F sao cho BE=EF=FD. Tính diện tích tứ giác AECFCho hình vuông ABCD có cạnh 12 cm. Trên đoạn BD lấy điểm E,F sao cho BE=EF=FD. Tính diện tích tứ giác AECFCho hình vuông ABCD có cạnh 12 cm. Trên đoạn BD lấy điểm E,F sao cho BE=EF=FD. Tính diện tích tứ giác AECFCho hình vuông ABCD có cạnh 12 cm. Trên đoạn BD lấy điểm E,F sao cho BE=EF=FD. Tính diện tích tứ giác AECF
Giải:
Ta có: \(BE=EF=FD=\frac{BD}{3}=\frac{12}{3}=4\left(cm\right)\)
\(S_{ABE}=\frac{BE\times AB}{2}\)
\(S_{CDF}=\frac{FD\times CD}{2}\)MÀ: BE = FD = 4cm; AB = CD = 12cm
\(\Rightarrow S_{ABE}=S_{CDF}=\frac{4\times12}{2}=24\left(cm^2\right)\)
DIỆN TÍCH HÌNH VUÔNG ABCD LÀ:
\(12\times12=144\left(cm^2\right)\)
DIỆN TÍCH AECF LÀ:
\(144-24\times2=144-48=96\left(cm^2\right)\)
Đ/S: 96cm2
Vì BE = EF = FD nên đoạn BD được chia thành 3 đoạn bằng nhau , mỗi đoạn dài :
12 : 3 = 4 ( cm )
Ta thấy AECF là hình tứ giác có đáy bé EF dài 4 cm , đáy lớn AC dài 12 cm , chiều cao AB = CD = 12 cm .
Vậy diện h AECF là :
( 4 + 12 ) x 12 : 2 = 96 ( cm2 )
Đáp số : 96 cm2 .