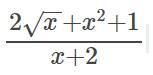 Rút gọn giúp mình với ạ
Rút gọn giúp mình với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(B=9x^4-\left(2x+1\right)^2-\left(9x^4+6x^2+1\right)\\ =9x^4-4x^2-4x-1-9x^4-6x^2-1\\ =-10x^2-4x-2\)


\(\dfrac{2sin8a-sin16a}{2sin8a+sin16a}=\dfrac{2sin8a-2sin8a.cos8a}{2sin8a+2sin8a.cos8a}=\dfrac{2sin8a\left(1-cos8a\right)}{2sin8a\left(1+cos8a\right)}=\dfrac{1-cos8a}{1+cos8a}=\dfrac{1-\left(1-2sin^24a\right)}{1+\left(1-2sin^24a\right)}=\dfrac{2sin^24a}{2-2sin^24a}=\dfrac{sin^24a}{1-sin^24a}=\dfrac{sin^24a}{cot^24a}=tan^24a\)
\(=\dfrac{2sin8a-2sin8a.cos8a}{2sin8a+2sin8a.cos8a}=\dfrac{2sin8a\left(1-cos8a\right)}{2sin8a\left(1+cos8a\right)}=\dfrac{1-cos8a}{1+cos8a}\)
\(=\dfrac{1-\left(1-2sin^24a\right)}{1+\left(2cos^24a-1\right)}=\dfrac{2sin^24a}{2cos^24a}=tan^24a\)

\(A=\left(\dfrac{2-x}{2+x}-\dfrac{16}{4-x^2}-\dfrac{2+x}{2-x}\right)\)
\(\Rightarrow A=\left(\dfrac{\left(2-x\right)^2}{\left(2+x\right)\left(2-x\right)}-\dfrac{16}{\left(2+x\right)\left(2-x\right)}-\dfrac{\left(2+x\right)^2}{\left(2+x\right)\left(2-x\right)}\right)\)\(\Rightarrow A=\left(\dfrac{4-4x+x^2}{\left(2+x\right)\left(2-x\right)}-\dfrac{16}{\left(2+x\right)\left(2-x\right)}-\dfrac{4+4x+x^2}{\left(2+x\right)\left(2-x\right)}\right)\)
\(\Rightarrow A=\dfrac{4-4x+x^2-16-4-4x-x^2}{\left(2+x\right)\left(2-x\right)}\)
\(\Rightarrow A=\dfrac{-8x-16}{\left(2+x\right)\left(2-x\right)}\)
\(\Rightarrow A=\dfrac{-8\left(x+2\right)}{\left(2+x\right)\left(2-x\right)}\)
\(\Rightarrow A=\dfrac{-8}{2-x}\)
\(\Rightarrow A=\dfrac{8}{x-2}\)

cảm ơn bạn nhưng bạn trình bày giúp mình được ko ạ mình cảm ơn:3

a) \(\sqrt{0,64.a^2}\left(a>0\right)=0,8.\left|a\right|=0,8a\)
b) \(\sqrt{a^2\left(a-2\right)^2}\left(a>2\right)=\left|a\left(a-2\right)\right|=a\left(a-2\right)=a^2-2a\)
c) \(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}\left(a\ge0,a\ne1\right)=\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}=1+\sqrt{a}+a\)

d: \(\dfrac{-\left(\sqrt{3}-\sqrt{6}\right)}{1-\sqrt{2}}+\dfrac{6\sqrt{3}+3}{\sqrt{3}}-\dfrac{13}{4+\sqrt{3}}\)
\(=-\sqrt{3}+6+\sqrt{3}-4+\sqrt{3}\)
\(=2+\sqrt{3}\)

\(P=\left(\dfrac{x-1}{\sqrt{x}+1}-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}}+1\right).\dfrac{1}{x\sqrt{x}+1}\)
\(=\left(\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+1}-\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)}+1\right).\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\left(\sqrt{x}-1-\dfrac{\sqrt{x}-1}{\sqrt{x}}+1\right).\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)+\sqrt{x}}{\sqrt{x}}.\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}.\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}=\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
Bài 2:
Ta có: \(P=\left(\dfrac{x-1}{\sqrt{x}+1}-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}}+1\right)\cdot\dfrac{1}{x\sqrt{x}+1}\)
\(=\left(\sqrt{x}-1-\dfrac{\sqrt{x}-1}{\sqrt{x}}+1\right)\cdot\dfrac{1}{x\sqrt{x}+1}\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{1}{x+\sqrt{x}}\)

\(\left(36-6x+x^2\right)\left(6+x\right)\)
= \(216+36x-36x-6x^2+6x^2+x^3\)
= \(x^3+216\)




ĐKXĐ: \(x\ge0\)
\(\dfrac{2\sqrt{x}+x^2+1}{x+2}=\dfrac{\left(\sqrt{x}+1\right)^2}{x+2}\)