bài 2 :cho tg ABC vuông tại A .K là tđ BC. kể KM vuông góc AB,KN vuông góc AC a) cm tg AMKN là hình chữ nhật
b)lấy E đối xứng vs K qua M. tg AKBE là hình j vì sao
c) lấy F đối xứng vs K qua N .cm BE //CF và BE=CF. Vẽ hình giúp mik luôn nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
Do đó: AMHN là hình chữ nhật
b: Xét ΔABC có
H là trung điểm của BC
HN//AB
Do đó: N là trung điểm của AC
Xét tứ giác AHCK có
N là trung điểm chung của AC và HK
nên AHCK là hình bình hành
mà AC\(\perp\)HK
nên AHCK là hình thoi

a: Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
nên ABEC là hình bình hành
b: ABEC là hình bình hành
=>AC//BE và AC=BE
AC=BE
AC=AD
Do đó: BE=AD
AC//BE
=>BE//AD
Xét tứ giác ADBE có
AD//BE
AD=BE
Do đó: ADBE là hình bình hành
c: ADBE là hình bình hành
=>AB cắt DE tại trung điểm của mỗi đường
=>N là trung điểm chung của AB và DE
=>NA=NB
d: Xét ΔBAC có BM/BC=BN/BA
nên MN//AC
MN//AC
AC\(\perp\)AB
Do đó: MN\(\perp AB\)

Lời giải:
a. Tứ giác $AMKN$ có 3 góc vuông $\widehat{A}=\widehat{M}=\widehat{N}=90^0$ nên $AMKN$ là hình chữ nhật.
b.
Xét tam giác $AEM$ và $AKM$ có:
$MA$ chung
$\widehat{AME}=\widehat{AMK}=90^0$
$EM=KM$ (do $E,K$ đối xứng nhau qua $M$)
$\Rightarrow \triangle AEM=\triangle AKM$ (c.g.c)
$\Rightarrow \widehat{EAM}=\widehat{KAM}(1)$
Tương tự:
$\triangle AKN=\triangle ADN$ (c.g.c)
$\Rightarrow \widehat{DAN}=\widehat{KAN}(2)$
Từ $(1); (2)\Rightarrow \widehat{EAM}+\widehat{MAN}+\widehat{DAN}=\widehat{KAM}+\widehat{MAN}+\widehat{KAN}=2\widehat{MAN}=2.90^0=180^0$
Hay $\widehat{EAD}=180^0$
$\Rightarrow E, A, D$ thẳng hàng.

a, Vì \(\widehat{EAD}=\widehat{ADM}=\widehat{AEM}=90^0\) nên ADME là hcn
Do đó \(AM=DE\)
b, Xét tg AMK có AE vừa là đường cao vừa là trung tuyến nên là tg cân
Do đó \(AM=AK=DE\)
Mà ADME là hcn nên \(AD=ME=EK\)
Do đó DEKA là hbh

BE=2*BA
DC=2*AC
mà AB=AC
nên BE=DC
Xét tứ giác BCED có
A là trung điểm chung của BE và CD
Do đó: BCED là hình bình hành
Hình bình hành BCED có BE=CD
nên BCED là hình chữ nhật

a: Xét tứ giác AMKN có
\(\widehat{AMK}=\widehat{ANK}=\widehat{NAM}=90^0\)
Do đó: AMKN là hình chữ nhật

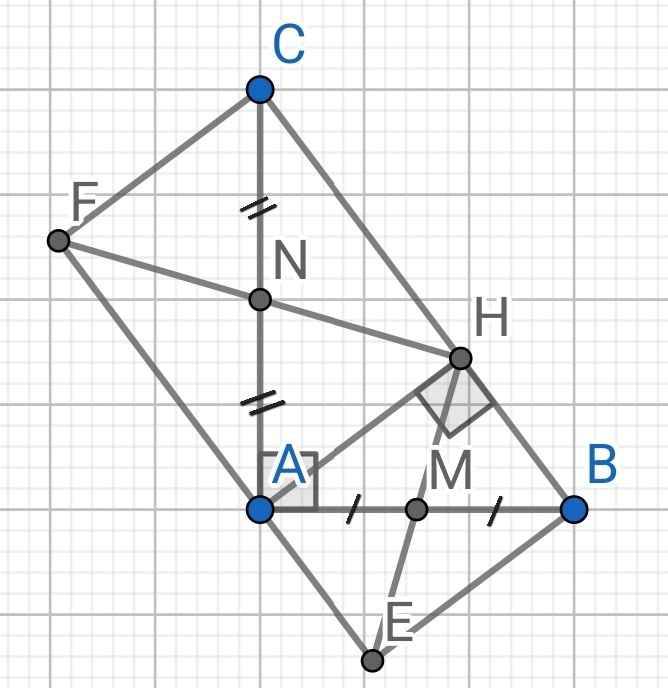 a) Do H và E đối xứng qua M (gt)
a) Do H và E đối xứng qua M (gt)
⇒ M là trung điểm HE
Tứ giác AHBE có:
M là trung điểm AB (gt)
M là trung điểm HE (cmt)
⇒ AHBE là hình bình hành
Lại có:
∠AHB = 90⁰ (AH ⊥ BC)
⇒ AHBE là hình chữ nhật
b) Do F và H đối xứng qua N
⇒ N là trung điểm của HF
Tứ giác AHCF có:
N là trung điểm AC (gt)
N là trung điểm HF (cmt)
⇒ AHCF là hình bình hành
⇒ AH = CF và AH // CF (1)
Do AHBE là hình chữ nhật (cmt)
⇒ AH // BE và AH = BE (2)
Từ (1) và (2) suy ra:
CF // BE và CF = BE
a: Xét tứ giác AMKN có
\(\widehat{AMK}=\widehat{ANK}=\widehat{MAN}=90^0\)
=>AMKN là hình chữ nhật
b: Xét ΔABC có
K là trung điểm của BC
KM//AC
Do đó: M là trung điểm của AB
Xét ΔABC có
K là trung điểm của BC
KN//AB
Do đó: N là trung điểm của AC
Xét tứ giác AKBE có
M là trung điểm chung của AB và KE
nên AKBE là hình bình hành
Xét hình bình hành AKBE có AB\(\perp\)KE
nên AKBE là hình thoi
c: Xét tứ giác AKCF có
N là trung điểm chung của AC và KF
nên AKCF là hình bình hành
=>CF//AK và CF=AK
AKBE là hình bình hành
=>BE//AK và BE=AK
BE//AK
CF//AK
Do đó: BE=CF
BE=AK
CF=AK
Do đó: BE=CF