Giúp mình bài này với ạ. Tìm x
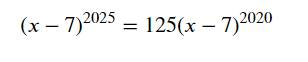
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


X x 2011 - X x 1 = 2011 x 2 +2009
X x ( 2011 - 1 ) = 4022 + 2009
X x 2010 = 6031
2010

Thay x = 2 vào phương trình ta có
\(\left(m+1\right)2-4=6\\ 2m+2=10\\ 2m=8\\ m=4\)
Vậy m = 4 để phương trình nhận x = 2 là nghiệm.

\(5x.\left(3x-2\right)=4-9x^2\)
\(\Rightarrow5x.\left(3x-2\right)-\left(4-9x^2\right)=0\)
\(\Rightarrow5x.\left(3x-2\right)+\left(9x^2-4\right)=0\)
\(\Rightarrow5x.\left(3x-2\right)+\left(3x-2\right).\left(3x+2\right)=0\)
\(\Rightarrow\left(3x-2\right).\left(5x+3x+2\right)=0\)
\(\Rightarrow\left(3x-2\right).\left(8x+2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x-2=0\\8x+2=0\end{cases}}\Rightarrow\orbr{\begin{cases}3x=2\\8x=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x=\frac{-1}{4}\end{cases}}\)

`@` `\text {Ans}`
`\downarrow`
`(8x-3)(3x+2)-(4x+7)(x+4)=(2x+1)(5x-1)-33`
`\Leftrightarrow 8x(3x+2) -3(3x+2) - 4x(x+4) + 7(x+4) = 2x(5x-1) + 5x-1 - 33`
`\Leftrightarrow 24x^2 + 16x - 9x - 6 - 4x^2 - 16x - 7x - 28 = 10x^2 - 2x + 5x - 1 - 33`
`\Leftrightarrow 20x^2 -16x - 34 = 10x^2 + 3x - 34`
`\Leftrightarrow 20x^2 - 16x - 34 - 10x^2 - 3x + 34 = 0`
`\Leftrightarrow 10x^2 - 19x = 0`
`\Leftrightarrow x(10x - 19)=0`
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\10x-19=0\end{matrix}\right.\)
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\10x=19\end{matrix}\right.\)
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\x=\dfrac{19}{10}\end{matrix}\right.\)
Vậy, `x={0; 19/10}.`

Vì |2x-3| - |3x+2| = 0
Suy ra |2x-3|=|3x+2|
Ta có 2 trường hợp:
+)Trường hợp 1: Nếu 2x-3=3x+2
2x-3=3x+2
-3-2=3x-2x
-2=x
+)Trường hợp 2: Nếu 2x-3=-(3x+2)
2x-3=-(3x+2)
2x-3=-3x-2
2x+3x=3-2
5x=1
x=1/5
Vậy x thuộc {-1,1/5}
(2x - 3) - ( 3x + 2) = 0
tính trong ngoặc trước ngoài ngoặc sau
2x - 3 ko phải là 2 nhân âm 3.
2x = 2 nhân x
( 2x - 3) - ( 3x + 2) = 0 có nghĩa là 2x -3 = 3x + 2
còn đâu tự giải nhé
\(\left(x-7\right)^{2025}=125\left(x-7\right)^{2020}\\ =>\left(x-7\right)^{2020}.\left[\left(x-7\right)^5-125\right]=0\)
\(=>\left[{}\begin{matrix}\left(x-7\right)^{2020}=0\\\left(x-7\right)^5=125\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x-7=0\\x-7=\sqrt[5]{125}\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x=7\\x=7+\sqrt[5]{125}\end{matrix}\right.\)
Lời giải:
$(x-7)^{2025}=125(x-7)^{2020}$
$\Rightarrow (x-7)^{2025}-125(x-7)^{2020}=0$
$\Rightarrow (x-7)^{2020}[(x-7)^5-125]=0$
$\Rightarrow (x-7)^{2020}=0$ hoặc $(x-7)^5=125$
$\Rightarrow x-7=0$ hoặc $x-7=sqrt[5]{125}+7$