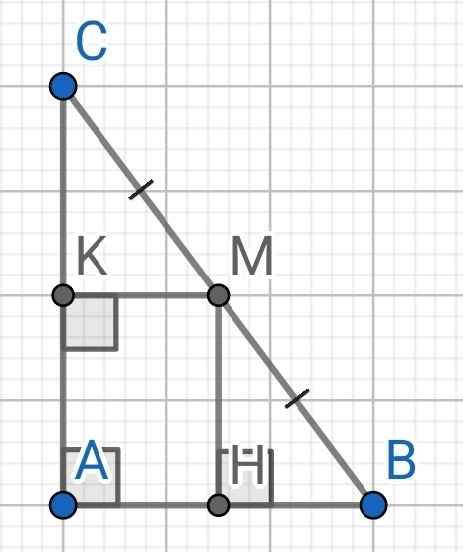
Cho ABC vuông tại A. có M là trung điểm của BC.Từ M kẻ MN vuông góc với AB tại N,MK vuông góc với AC tại K(N thuộc AB,K thuộc AC)
a)Tứ giác ANMK là hình gì?vì sao?
b)Gọi O là trung điểm của MK.Chứng minh:ON=OC.
c)E đối xứng với M qua N.Chứng minh:AM,KN và EC đồng quy.

a) Xét tứ giác ANMK có:
\(\left\{{}\begin{matrix}\widehat{A}=90^o\\\widehat{N}=90^o\\\widehat{K}=90^o\end{matrix}\right.\)
=> ANMK là hình chữ nhật
b) Ta có:
\(\widehat{MCA}=\widehat{MAC}=\widehat{NAK}\) mà 2 góc có vị trí đồng vị
=> NK//MC
Mặt khác: MN//KC
=> NMCK là hình bình hành
Ta có: O là trung điểm MK
=> O là trung điểm NC
=> ON=OC
c)
Vì tứ giác ANMK là hình chữ nhật
=> NM=AK
tứ giác NMCK là hình bình hành
=> NM=KC
=> \(MN=\dfrac{1}{2}AC\)
\(\Rightarrow EM=AC\)
mà EM//AC
=> AEMC là hình bình hành
Gọi I là trung điểm AM
=> I là trung điểm EC
Vì ANMK là h.c.n
=> I là trung điểm NK
=> AM, NK, EC đồng quy tại I