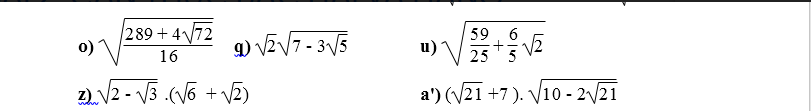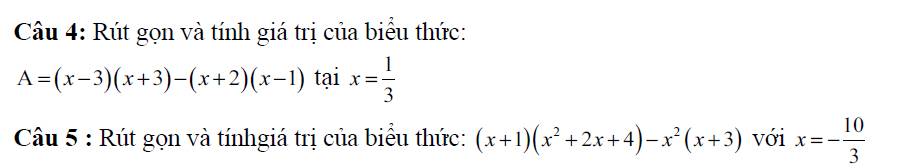 Giải chi tiết 2 bài với ạ. Cần gấp. Cảm ơn ạ.
Giải chi tiết 2 bài với ạ. Cần gấp. Cảm ơn ạ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)


a. Điện trở tương đương của mạch là: \(R_{tđ}=\dfrac{U}{I}=\dfrac{6}{0,5}=12\Omega\)
b. Giá trị điện trở R2 là: \(R_2=R_{tđ}-R_1=12-5=7\Omega\)
a)Rtđ=\(\dfrac{U}{I}=\dfrac{6}{0,5}=12\left(\Omega\right)\)
b)Vì R1 nối tiếp với R2
R2=Rtđ-R1=12-5=7(\(\Omega\))

3.
\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)
\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)
\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)
\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
4.
\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)
\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)
\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)
\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)

a: Xét tứ giác AECF có
AE//CF(AB//CD)
AE=CF
Do đó: AECF là hình bình hành
b: AE+EB=AB
CF+FD=CD
mà AE=CF và AB=CD
nên BE=DF
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>DE=BF
c:
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔAIC có
D,O lần lượt là trung điểm của AI,AC
=>DO là đường trung bình
=>DO//CI
d: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của EF
=>AC,EF,BD đồng quy(do cùng đi qua O)

a) \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
b) \(=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\)
c) \(=\sqrt{\left(2\sqrt{2}+3\right)^2}=2\sqrt{2}+3\)
d) \(=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}\)
e) \(=\sqrt{\left(4-\sqrt{6}\right)^2}=4-\sqrt{6}\)
f) \(=\sqrt{\left(3+\sqrt{7}\right)^2}=3+\sqrt{7}\)
l) \(=\sqrt{\left(\sqrt{2}-\dfrac{1}{2}\right)^2}=\sqrt{2}-\dfrac{1}{2}\)
m) \(=\sqrt{\left(2\sqrt{2}+\dfrac{1}{4}\right)^2}=2\sqrt{2}+\dfrac{1}{4}\)








 Giải hết và chi tiết với ạ. Em đang cần gấp ạ. Em cảm ơn nhiều ạ.
Giải hết và chi tiết với ạ. Em đang cần gấp ạ. Em cảm ơn nhiều ạ.
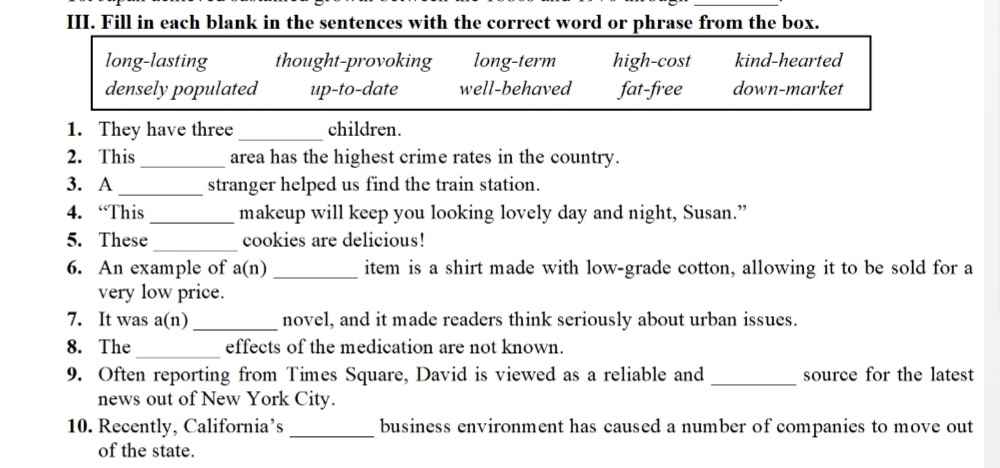


 Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn