Qua trung điểm M của đoạn thẳng AB , kẻ dường thẳng vuông góc với AB. Trên dường thẳng đó lấy K . CHứng minh răng KM là tia phân giác của góc AKB
Nhớ viết giả thiết và kết luận giùm mk lun nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
22 tháng 11 2016
Ta có hình vẽ sau:
Ta có: \(\widehat{M_1}\) + \(\widehat{M_2}\) = 180o hay \(\widehat{M_1}\) + 90o = 180o
\(\Rightarrow\) \(\widehat{M_1}\) = 180o - 90o = 90o
\(\Rightarrow\) \(\widehat{M_1}\) = \(\widehat{M_2}\) = 90o
Xét ΔKAM và ΔKBM có:
KM: Cạnh chung
\(\widehat{M_1}\) = \(\widehat{M_2}\) = 90o (cm trên)
AM = BM (gt)
\(\Rightarrow\) ΔKAM = ΔKBM (c.g.c)
\(\Rightarrow\) \(\widehat{K_1}\) = \(\widehat{K_2}\) (2 góc tương ứng)
\(\Rightarrow\) KM là tia phân giác của \(\widehat{AKB}\) (đpcm)
22 tháng 11 2016
Gọi đường thẳng đó là x
Ta có hình vẽ:
Vì \(\widehat{AMK}\) +\(\widehat{BMK}\) = 1800 (kề bù)
Mà KM \(\perp\)AB => \(\widehat{AMK}\)=\(\widehat{BMK}\)=\(\frac{180^0}{2}\)=900
Vậy KM là phân giác góc AKB (đpcm)
CM
6 tháng 4 2019
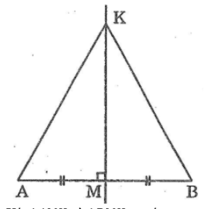
Xét ΔAMK và ΔBMK, ta có:
AM = BM (gt)
∠(AMK) =∠(BMK) =90o (vì KM⊥AB)
MK cạnh chung
Suy ra: ΔAMK= ΔBMK(c.g.c)
⇒∠(AKM) =∠(BKM)
Vậy KM là tia phân giác của góc AKB
LA
20 tháng 11 2016
Ta có hình vẽ :
Xét 2 tam giác KAM và KBM ta có :
AM = BM
KM chung
AMK = BMK = 90 độ
\(\Rightarrow\)Tam giác AMK = Tam giác BMK
\(\Rightarrow\)AKM = BKM
\(\Rightarrow\)KM là phân giác của góc AKB .
Vì M là trunng điểm của AB
Mà MK vuông góc với AB
=>MK là đường trung trực ứng với AB
=>KA=KB
=>\(\Delta AKC\)cân tại A
Xét \(\Delta AKB\)có KM là đường trung trực ứng với ab đồng thời là đường phân giác
=> KM là tia phân giác góc AKB
GT:đoạn thẳng AB ;M\(\in\)AB(MA=MB);d\(⊥\)BA;M\(\in\)d;k\(\in\)d
KL:\(\widehat{AKM}=\widehat{BKM}\)
CM
ta có đường thẳng d vừa đi qua trung điểm của đoạn thẳng vừa vuông góc với đoạn thẳng AB
=>d là đường trung trực của AB
=> K cách đều hai đầu mút A và B ( tc đường trung trực)
=>KA=KB
=>tam giác AKB cân tại K
=> KM là đường trung trực đồng thời là phân giác