Cho $\Delta ABC$ vuông cân tại $A.$ Gọi $M$ là trung điểm của $BC.$ Trên tia đối của tia $MA$ lấy điểm $D$ bất kì. Từ $D$ kẻ các đường thẳng vuông góc với $AB, \, AC$ lần lượt tại $E, \, F.$
a) Chứng minh $AEDF$ là hình vuông.
b) Chứng minh $EF$ // $BC.$
c) Qua $E$ kẻ đường thẳng vuông góc với $MF$ tại $N.$ Chứng minh...
Đọc tiếp
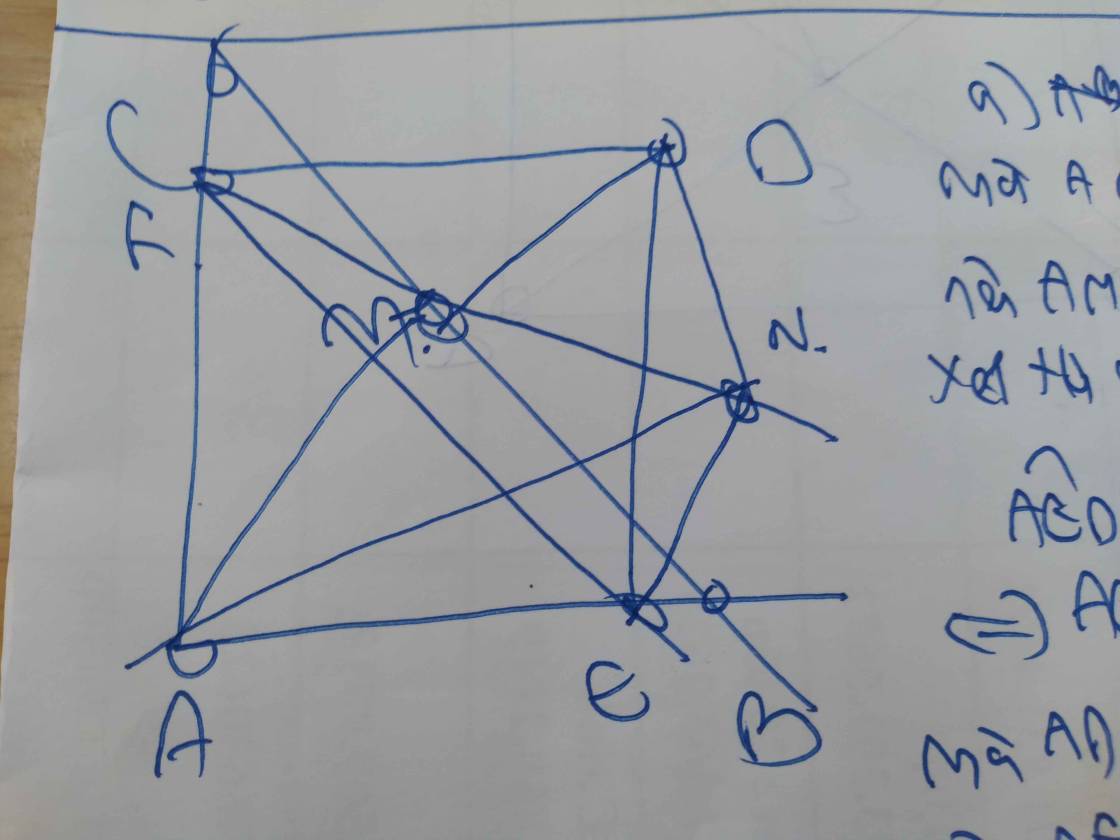
Cho $\Delta ABC$ vuông cân tại $A.$ Gọi $M$ là trung điểm của $BC.$ Trên tia đối của tia $MA$ lấy điểm $D$ bất kì. Từ $D$ kẻ các đường thẳng vuông góc với $AB, \, AC$ lần lượt tại $E, \, F.$
a) Chứng minh $AEDF$ là hình vuông.
b) Chứng minh $EF$ // $BC.$
c) Qua $E$ kẻ đường thẳng vuông góc với $MF$ tại $N.$ Chứng minh $\widehat{AND}={{90}^{\circ}}.$
a: ΔABC vuông cân tại A
mà AM là trung tuyến
nên AM là phân giác của góc BAC
Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
AD là phân giác của góc FAE
=>AEDF là hình vuông
b: AEDF là hình vuông
=>góc AEF=45 độ
=>góc AEF=góc ABC
=>EF//BC
a) AEDF là hình vuông.
b) ��EF // ��.BC.
c) ���^=90∘.AND=90∘.