Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là phân giác của \(\widehat{BAC}\)
Xét tứ giác AMEN có \(\widehat{AME}=\widehat{ANE}=\widehat{MAN}=90^0\)
=>AMEN là hình chữ nhật
Xét hình chữ nhật AMEN có AE là phân giác của \(\widehat{MAN}\)
nên AMEN là hình vuông
b: AMEN là hình vuông
=>\(\widehat{AMN}=45^0\)
=>\(\widehat{AMN}=\widehat{ABC}\)
mà hai góc này ở vị trí đồng vị
nên MN//BC
c: AMEN là hình vuông
=>A,M,E,N cùng thuộc đường tròn tâm O, đường kính là AE và MN
=>O là trung điểm chung của AE và MN(2)
\(\widehat{MFN}=90^0\)
=>F nằm trên đường tròn đường kính MN
=>F nằm trên (O)
Xét (O) có
ΔAFE nội tiếp
AE là đường kính
Do đó: ΔAFE vuông tại F
=>\(\widehat{AFE}=90^0\)

a: Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
AD là phân giác của góc EAF
Do đó: AEDF là hình vuông
b: Vì AEDF là hình vuông thì góc AEF=45 độ=góc ABC
=>EF//BC

a: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là phân giác của góc BAC
Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
Hình chữ nhật AEDF có AD là phân giác của góc FAE
nên AEDF là hình vuông
b: AEDF là hình vuông
=>\(\widehat{AEF}=45^0\)
=>\(\widehat{AEF}=\widehat{ABC}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên FE//BC

a: Xét ΔBED vuông tại E và ΔBAC vuông tại A có
góc B chung
=>ΔBED đồng dạng vơi ΔBAC
b: Xet ΔCAB co FD//AB
nên DB/DC=FA/FC
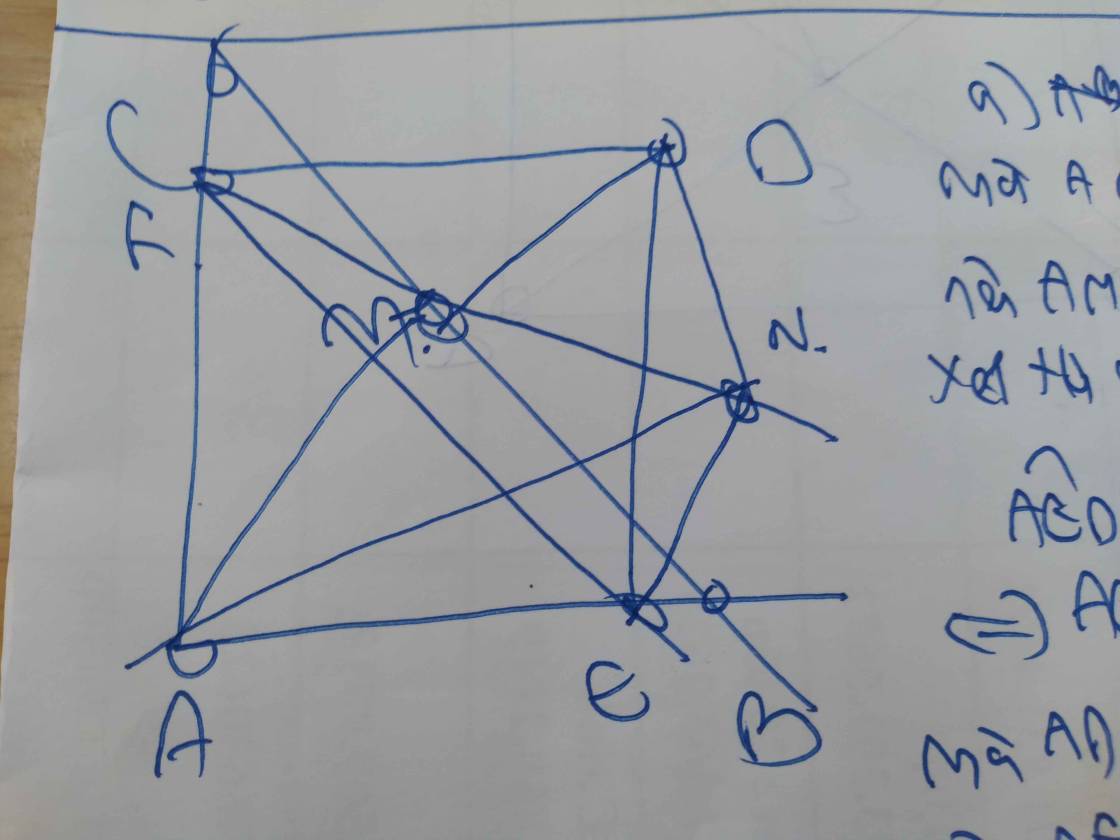


a: ΔABC vuông cân tại A
mà AM là trung tuyến
nên AM là phân giác của góc BAC
Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
AD là phân giác của góc FAE
=>AEDF là hình vuông
b: AEDF là hình vuông
=>góc AEF=45 độ
=>góc AEF=góc ABC
=>EF//BC