làm hộ mk bài 1.3 thôi ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1)
a) 4y2-4xy+x2= x2-4xy+4y2= (x-2y)2
b) 9x2-12xy+4y2= (3x)2-2.3x.2y+(2y)2= (3x-2y)2
c) 16x2-25=(4x)2-52= (4x-5)(4x+5)
d) 1-9y2= 12-(3y)2=(1-3y)(1+3y)
g) x3-27y3= (x-3y)(x2+3xy+9y2)
h) 64 + 8x3=(4+2x)(16+8x+4x2)

Bài 5:
e: \(\dfrac{2}{x+1}=\dfrac{2x^2-2x+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(\dfrac{3}{x^2-x+1}=\dfrac{3x+3}{\left(x+1\right)\left(x^2-x+1\right)}\)

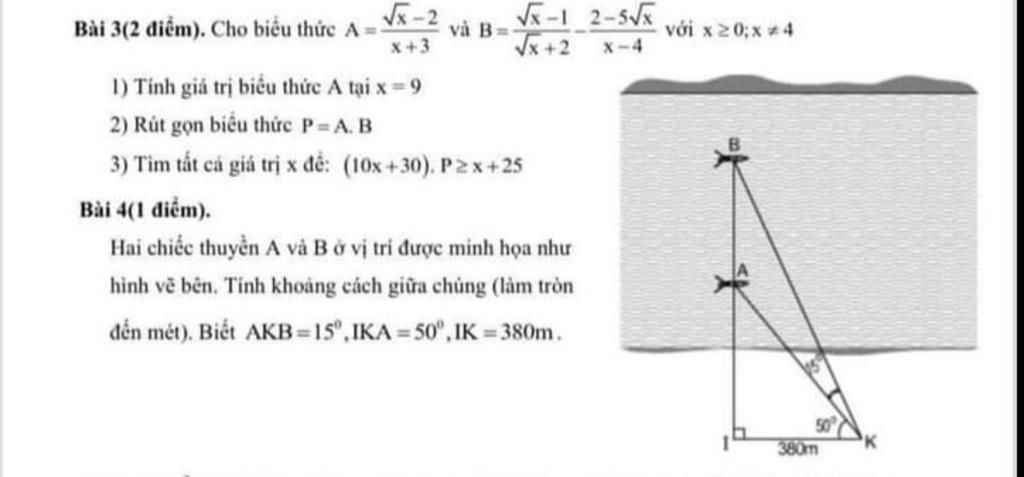
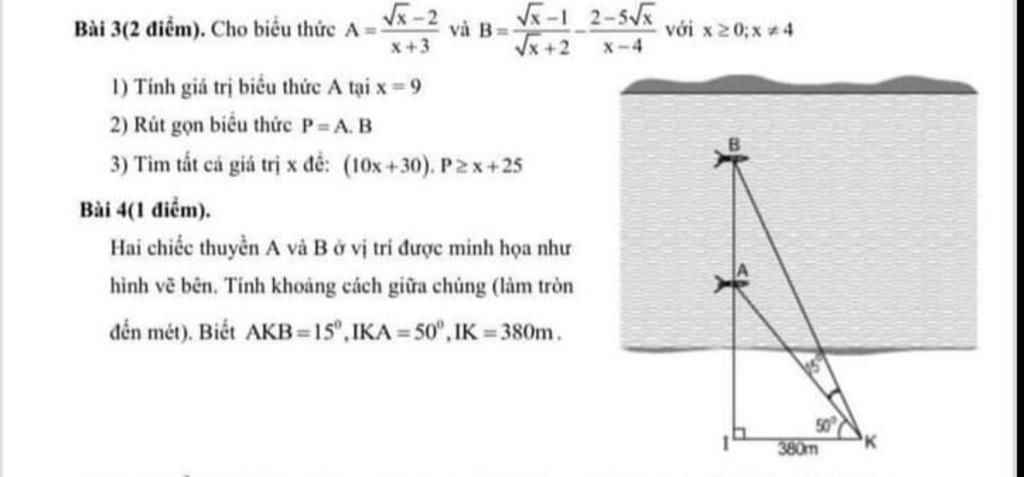
Bài 3:
a: Thay x=9 vào A, ta được:
\(A=\dfrac{3-2}{3+3}=\dfrac{1}{6}\)

Bài 3:
\(1,x=9\Leftrightarrow A=\dfrac{3-2}{9+3}=\dfrac{1}{12}\\ 2,P=AB=\dfrac{\sqrt{x}-2}{x+3}\cdot\dfrac{x-3\sqrt{x}+2-2+5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(x+3\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{x+3}\\ 3,\left(10x+30\right)P\ge x+25\\ \Leftrightarrow\dfrac{3\sqrt{x}\left(x+3\right)}{x+3}-x-25\ge0\\ \Leftrightarrow3\sqrt{x}-x-25\ge0\\ \Leftrightarrow-\left(x-3\sqrt{x}+\dfrac{9}{4}\right)-\dfrac{91}{4}\ge0\\ \Leftrightarrow-\left(\sqrt{x}-\dfrac{3}{2}\right)^2-\dfrac{91}{4}\ge0\left(vô.lí\right)\\ \Leftrightarrow x\in\varnothing\)

Bài 12:
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN

Tự làm,bài tập về nhà không tự suy nghĩ lại đăng lên để người khác làm hộ à.Học phải có tư duy.

a)Ta có: \(\text{87 - 218 = (23)7 - 218 = 221 – 218 = 217.( 24 -2)= 217.(16 - 2) = 24.14 ⋮ 14}\)

(O) và (D) cắt nhau tại A và M \(\Rightarrow AM\perp OD\)
\(\Rightarrow\widehat{AOD}=\widehat{ABN}\) (cùng phụ \(\widehat{BAM}\))
\(\Rightarrow OD||BN\) (góc đồng vị bằng nhau)
\(\Rightarrow OBND\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow OB=DN\), mà \(\left\{{}\begin{matrix}AB=DC\\OB=\dfrac{1}{2}AB\end{matrix}\right.\) \(\Rightarrow OB=\dfrac{1}{2}CD\Rightarrow DN=\dfrac{1}{2}DC\Rightarrow N\) là trung điểm CD






 Like cho mình nhé !!
Like cho mình nhé !!
1.3:
a: BE là phân giác của \(\widehat{ABD}\)
=>\(\widehat{ABE}=\widehat{DBE}=\dfrac{\widehat{CBD}}{2}=\dfrac{80^0}{2}=40^0\)
b: \(\widehat{ABE}=40^0\)
mà \(A\in BC\)
nên \(\widehat{EBC}=40^0\)