Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Dựa vào đồ thị ta thấy \({x^2} + 2,5x - 1,5 \le 0\) khi x thuộc đoạn \(\left[ { - 3;\frac{1}{2}} \right]\)
Vậy nghiệm của bất phương trình \({x^2} + 2,5x - 1,5 \le 0\) là \(\left[ { - 3;\frac{1}{2}} \right]\)
b) Dựa vào đồ thị ta thấy \( - {x^2} - 8x - 16 < 0\) với mọi x khác \( - 4\)
Vậy nghiệm của bất phương trình \( - {x^2} - 8x - 16 < 0\) là \(\mathbb{R}\backslash \left\{ { - 4} \right\}\)
c) Dựa vào đồ thị ta thấy \( - 2{x^2} + 11x - 12 > 0\) khi x thuộc khoảng \(\left( {\frac{3}{2};4} \right)\)
Vậy nghiệm của bất phương trình \( - 2{x^2} + 11x - 12 > 0\) là \(\left( {\frac{3}{2};4} \right)\)
d) Dựa vào đồ thị ta thấy đồ thị của tam thức \(f\left( x \right) = \frac{1}{2}{x^2} + \frac{1}{2}x + 1\) nằm hoàn toàn phía trên trục hoành với mọi x
Vậy bất phương trình \(\frac{1}{2}{x^2} + \frac{1}{2}x + 1 \le 0\) vô nghiệm.

Hình 30a:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \left( { - \infty ;1} \right) \cup \left( {4; + \infty } \right)\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \left( {1;4} \right)\)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \left( { - \infty ;1} \right] \cup \left[ {4; + \infty } \right)\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left[ {1;4} \right]\)
Hình 30b:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\backslash \left\{ 2 \right\}\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left\{ 2 \right\}\)
Hình 30c:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \emptyset \)

a) Tam thức \(f\left( x \right) = {x^2} + 1,5x - 1\) có hai nghiệm phân biệt \({x_1} = - 2;{x_2} = \frac{1}{2}\)
\(\)\(f\left( x \right) > 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{1}{2}, + \infty } \right)\) và \(f\left( x \right) < 0\) khi \(x \in \left( { - 2,\frac{1}{2}} \right)\)
Ta có bảng xét dấu như sau

b) Tam thức \(g\left( x \right) = {x^2} + x + 1\) vô nghiệm, \(g\left( x \right) > 0\forall x \in \mathbb{R}\)
Ta có bảng xét dấu như sau

c) Tam thức \(h\left( x \right) = - 9{x^2} - 12x - 4\) có nghiệm kép \({x_1} = {x_2} = - \frac{2}{3}\) và \(h\left( x \right) < 0\forall x \ne - \frac{2}{3}\)
Ta có bảng xét dấu như sau

d) Tam thức \(f\left( x \right) = - 0,5{x^2} + 3x - 6\) vô nghiệm và \(f\left( x \right) < 0\forall x \in \mathbb{R}\)
Ta có bảng xét dấu như sau:

e) Tam thức \(g\left( x \right) = - {x^2} - 0,5x + 3\) có hai nghiệm \({x_1} = - 2,{x_2} = \frac{3}{2}\)
\(g\left( x \right) > 0\) khi \(x \in \left( { - 2,\frac{3}{2}} \right)\) và \(g\left( x \right) < 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{3}{2}, + \infty } \right)\)
Ta có bảng xét dấu như

g) Tam thức \(h\left( x \right) = {x^2} + 2\sqrt 2 x + 2\) có nghiệm kép \({x_1} = {x_2} = - \sqrt 2 \)
\(h\left( x \right) > 0\forall x \ne - \sqrt 2 \)
Ta có bảng xét dấu như sau


Số nghiệm của phương trình x 3 = b là số giao điểm của hai đồ thị hàm số y = b và y = x 3 .
Dựa vào H26 ta có đồ thị hàm số y = x 3 luôn cắt đường thẳng y = b tại một điểm duy nhất với mọi b nên phương trình x 3 = b luôn có nghiệm duy nhất với mọi b.
Số nghiệm của phương trình x 4 = b (1) là số giao điểm của hai đồ thị hàm số y = b và y = x 4 . Dựa và hình 27 ta có:
+ Với b < 0 hai đồ thị hàm số trên không giao nhau, vậy phương trình (1) vô nghiệm.
+ Với b = 0, hai đồ thị hàm số tiếp xúc nhau tại (0,0), vậy phương trình (1) có nghiệm duy nhất x = 0.
+ Với b > 0, hai đồ thị hàm số cắt nhau tại hai điểm phân biết, vậy phương trình (1) có hai nghiệm phân biệt.

Pt hoành độ giao điểm:
\(-x^2+2x+3=-2x+1\)
\(\Leftrightarrow x^2-4x-2=0\Rightarrow\left[{}\begin{matrix}x=2+\sqrt{6}\Rightarrow y=-3-2\sqrt{6}\\x=2-\sqrt{6}\Rightarrow y=-3+2\sqrt{6}\end{matrix}\right.\)
Vậy tọa độ giao điểm là: \(\left(2+\sqrt{6};-3-2\sqrt{6}\right)\)
Và \(\left(2-\sqrt{6};-3+2\sqrt{6}\right)\)
\(\left(P\right):y=-x^2+2x+3\\ \left(d\right):y=-2x+1\)
xét phương trình hoành độ giao điểm của (P) và (d)
\(-x^2+2x+3=-2x+1\)
\(< =>-x^2+4x+2=0\)
\(< =>\left[{}\begin{matrix}x=2+\sqrt{6}\\x=2-\sqrt{6}\end{matrix}\right.\)
thay vào (d) => \(\left[{}\begin{matrix}x=2+\sqrt{6}=>y=-3-2\sqrt{6}\\x=2-\sqrt{6}=>y=-3+2\sqrt{6}\end{matrix}\right.\)
vậy ...

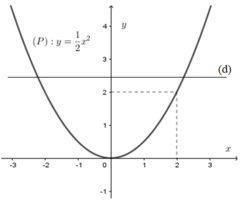
Xét phương trình x2 – 2m + 4 = 0 (*)
⇔ x2 = 2m – 4 ⇔ 1 2 x 2 = m − 2
Số nghiệm của phương trình (*) là
số giao điểm của parabol (P): y = 1 2 x 2
và đường thẳng d: y = m – 2
Để (*) có hai nghiệm phân biệt thì d cắt (P) tại hai điểm phân biệt
Từ đồ thị hàm số ta thấy:
Với m – 2 > 0 ⇔ m > 2 thì d cắt (P)
tại hai điểm phân biệt hay phương trình (*)
có hai nghiệm phân biệt khi m > 2
Đáp án cần chọn là: A

Ta có 2x2 – m – 5 = 0 (*)
⇔ 2x2 = m + 5
Số nghiệm của phương trình (*) là số giao điểm của
parabol (P): y = 2x2và đường thẳng d: y = m + 5
Để (*) có hai nghiệm phân biệt thì d cắt (P) tại
hai điểm phân biệt.Từ đồ thị hàm số ta thấy:
Với m + 5 > 0 ⇔ m > −5 thì d cắt (P)
tại hai điểm phân biệt hay phương trình (*)
có hai nghiệm phân biệt khi m > −5
Đáp án cần chọn là: D
a) Quan sát vào độ thị ta thấy đoạn mà đồ thị nằm dưới truch hoành là \(\left[ { - 2;\frac{5}{2}} \right]\)
Vậy nghiệm của bất phương trình \({x^2} - 0,5x - 5 \le 0\) là đoạn \(\left[ { - 2;\frac{5}{2}} \right]\)
b) Quan sát vào đồ thị ta thấy đồ thị luôn nằm dưới trục hoành
Vậy nghiệm của bất phương trình \( - 2{x^2} + x - 1 > 0\) vô nghiệm