Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Dựa vào đồ thị ta thấy \({x^2} + 2,5x - 1,5 \le 0\) khi x thuộc đoạn \(\left[ { - 3;\frac{1}{2}} \right]\)
Vậy nghiệm của bất phương trình \({x^2} + 2,5x - 1,5 \le 0\) là \(\left[ { - 3;\frac{1}{2}} \right]\)
b) Dựa vào đồ thị ta thấy \( - {x^2} - 8x - 16 < 0\) với mọi x khác \( - 4\)
Vậy nghiệm của bất phương trình \( - {x^2} - 8x - 16 < 0\) là \(\mathbb{R}\backslash \left\{ { - 4} \right\}\)
c) Dựa vào đồ thị ta thấy \( - 2{x^2} + 11x - 12 > 0\) khi x thuộc khoảng \(\left( {\frac{3}{2};4} \right)\)
Vậy nghiệm của bất phương trình \( - 2{x^2} + 11x - 12 > 0\) là \(\left( {\frac{3}{2};4} \right)\)
d) Dựa vào đồ thị ta thấy đồ thị của tam thức \(f\left( x \right) = \frac{1}{2}{x^2} + \frac{1}{2}x + 1\) nằm hoàn toàn phía trên trục hoành với mọi x
Vậy bất phương trình \(\frac{1}{2}{x^2} + \frac{1}{2}x + 1 \le 0\) vô nghiệm.
QT
1
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Quan sát vào độ thị ta thấy đoạn mà đồ thị nằm dưới truch hoành là \(\left[ { - 2;\frac{5}{2}} \right]\)
Vậy nghiệm của bất phương trình \({x^2} - 0,5x - 5 \le 0\) là đoạn \(\left[ { - 2;\frac{5}{2}} \right]\)
b) Quan sát vào đồ thị ta thấy đồ thị luôn nằm dưới trục hoành
Vậy nghiệm của bất phương trình \( - 2{x^2} + x - 1 > 0\) vô nghiệm
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
Hình 24a:
Ta thấy đồ thị cắt trục Ox tại điểm (2;0)
=> Phương trình \(f\left( x \right) = 0\) có nghiệm duy nhất \(x = 2\)
Ta thấy đồ thị nằm trên trục hoành nên có bảng xét dấu:
Hình 24b:
Ta thấy đồ thị cắt trục Ox tại 2 điểm phân biệt (-4;0) và (-1;0)
=> Phương trình \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = - 4,x = - 1\)
Trong các khoảng \(\left( { - \infty ; - 4} \right)\) và \(\left( { - 1; + \infty } \right)\) thì đồ thị nằm dưới trục hoành nên \(f\left( x \right) < 0\)
Trong khoảng \(\left( { - 4; - 1} \right)\) thì đồ thị nằm trên trục hoành nên \(f\left( x \right) > 0\)
Bảng xét dấu:
Hình 24c:
Ta thấy đồ thị cắt trục Ox tại 2 điểm phân biệt (-1;0) và (2;0)
=> Phương trình \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = - 1,x = 2\)
Trong các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {2; + \infty } \right)\) thì đồ thị nằm trên trục hoành nên \(f\left( x \right) > 0\)
Trong khoảng \(\left( { - 1;2} \right)\) thì đồ thị nằm dưới trục hoành nên \(f\left( x \right) < 0\)
Bảng xét dấu:
CM
10 tháng 3 2018
Đáp án: A
Từ bảng xét dấu ta thấy phương trình f(x) = 0 có 2 nghiệm là -3 và 2. Do đó, ta loại được đáp án C và D
Dựa vào bảng xét dấu, f(x) > 0 trong khoảng (-3;2) do đó hệ số a < 0
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 2} \right) = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = 1\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 1} \right) = 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 1;{x_2} = 3\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).3 = 16 > 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
Đồ thị nằm trên trục hoành với mọi \(x \in \left( { - 1,3} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm
Biệt thức \(\Delta = {6^2} - 4.1.10 = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi \(x\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = - 3\)
Biệt thức \(\Delta = {6^2} - 4.1.9 = 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 4;{x_2} = - 2\)
Biệt thức \(\Delta = {6^2} - 4.1.8 = 4 > 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
Đồ thị nằm dưới trục hoành với mọi \(x \in \left( { - 4, - 2} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
QT
1
23 tháng 9 2023
Tham khảo:
Tam thức bậc hai \(f\left( x \right) = - {x^2} - 2x + 8\) có hai nghiệm phân biệt \({x_1} = - 4,{x_2} = 2\) và hệ số \(a = - 1 < 0\).
Ta có bảng xét dấu \(f\left( x \right)\) như sau:
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
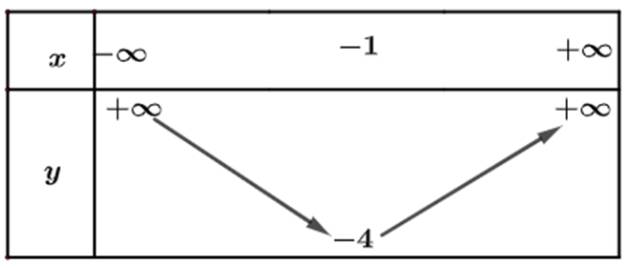
a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
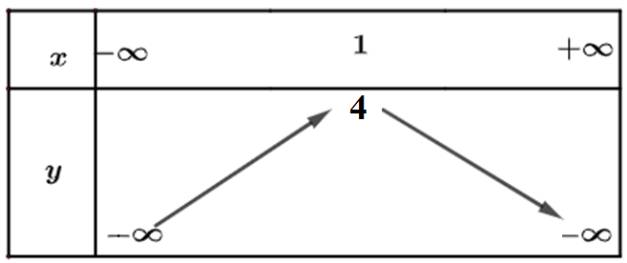
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
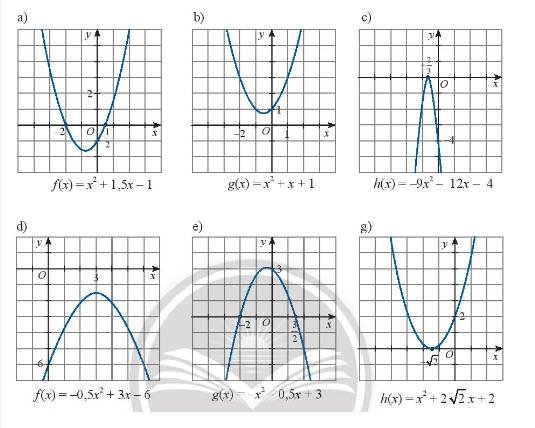
a) Tam thức \(f\left( x \right) = {x^2} + 1,5x - 1\) có hai nghiệm phân biệt \({x_1} = - 2;{x_2} = \frac{1}{2}\)
\(\)\(f\left( x \right) > 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{1}{2}, + \infty } \right)\) và \(f\left( x \right) < 0\) khi \(x \in \left( { - 2,\frac{1}{2}} \right)\)
Ta có bảng xét dấu như sau
b) Tam thức \(g\left( x \right) = {x^2} + x + 1\) vô nghiệm, \(g\left( x \right) > 0\forall x \in \mathbb{R}\)
Ta có bảng xét dấu như sau
c) Tam thức \(h\left( x \right) = - 9{x^2} - 12x - 4\) có nghiệm kép \({x_1} = {x_2} = - \frac{2}{3}\) và \(h\left( x \right) < 0\forall x \ne - \frac{2}{3}\)
Ta có bảng xét dấu như sau
d) Tam thức \(f\left( x \right) = - 0,5{x^2} + 3x - 6\) vô nghiệm và \(f\left( x \right) < 0\forall x \in \mathbb{R}\)
Ta có bảng xét dấu như sau:
e) Tam thức \(g\left( x \right) = - {x^2} - 0,5x + 3\) có hai nghiệm \({x_1} = - 2,{x_2} = \frac{3}{2}\)
\(g\left( x \right) > 0\) khi \(x \in \left( { - 2,\frac{3}{2}} \right)\) và \(g\left( x \right) < 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{3}{2}, + \infty } \right)\)
Ta có bảng xét dấu như
g) Tam thức \(h\left( x \right) = {x^2} + 2\sqrt 2 x + 2\) có nghiệm kép \({x_1} = {x_2} = - \sqrt 2 \)
\(h\left( x \right) > 0\forall x \ne - \sqrt 2 \)
Ta có bảng xét dấu như sau