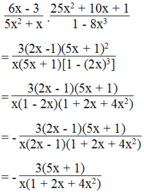Tìm x để A= 25x2 + 3y2 - 10x + 11
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 10 2023
\(a,\\ A=25x^2-10x+11\\ =\left(5x\right)^2-2.5x.1+1^2+10\\ =\left(5x+1\right)^2+10\ge10\forall x\in R\\ Vậy:min_A=10.khi.5x+1=0\Leftrightarrow x=-\dfrac{1}{5}\\ B=\left(x-3\right)^2+\left(11-x\right)^2\\ =\left(x^2-6x+9\right)+\left(121-22x+x^2\right)\\ =x^2+x^2-6x-22x+9+121=2x^2-28x+130\\ =2\left(x^2-14x+49\right)+32\\ =2\left(x-7\right)^2+32\\ Vì:2\left(x-7\right)^2\ge0\forall x\in R\\ Nên:2\left(x-7\right)^2+32\ge32\forall x\in R\\ Vậy:min_B=32.khi.\left(x-7\right)=0\Leftrightarrow x=7\\Tương.tự.cho.biểu.thức.C\)
15 tháng 10 2023
b:
\(D=-25x^2+10x-1-10\)
\(=-\left(25x^2-10x+1\right)-10\)
\(=-\left(5x-1\right)^2-10< =-10\)
Dấu = xảy ra khi x=1/5
\(E=-9x^2-6x-1+20\)
\(=-\left(9x^2+6x+1\right)+20\)
\(=-\left(3x+1\right)^2+20< =20\)
Dấu = xảy ra khi x=-1/3
\(F=-x^2+2x-1+1\)
\(=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1< =1\)
Dấu = xảy ra khi x=1
PT
1
CM
23 tháng 5 2018
Hướng dẫn giải:
Điều kiện xác định của phân thức: x ≠ 0 , x ≠ 5
Ta có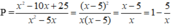 
Để P nhận giá trị nguyên thì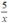 
nguyên. Hay x là ước của 5. Ta có Ư(5) = { 1;-1;5;-5}.
Vì điều kiện xác định của phân thức là x ≠ 0, x≠ 5
Vậy x ∈ { 1;-1;-5} thì giá trị phân thức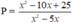 
là nguyên
PT
1
CM
10 tháng 1 2018
Biểu thức x 2 - 25 x 2 - 10 x + 25 x xác định khi x 0 và x ≠ 5.
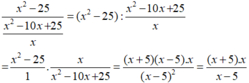
Ta có: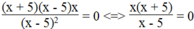 
khi x(x + 5) = 0 và x – 5
≠
0
x(x + 5) = 0 ⇔ x = 0 hoặc x + 5 = 0 ⇔ x = - 5
x = 0 không thỏa mãn điều kiện.
Vậy x = - 5 thì biểu thức x 2 - 25 x 2 - 10 x + 25 x có giá trị bằng 0.
CM
13 tháng 8 2017
Biểu thức x 2 - 25 x 2 + 10 x + 25 x - 5 xác định khi x ≠ 5 và x ≠ - 5
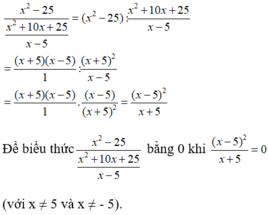
x - 5 2 = 0 ⇔ x – 5 = 0 ⇔ x= 5
x = 5 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để biểu thức x 2 - 25 x 2 + 10 x + 25 x - 5 có giá trị bằng 0.
CM
5 tháng 1 2017
Biểu thức x 2 - 25 x 2 - 10 x + 25 x xác định khi x 2 - 10 x + 25 ≠ 0 và x ≠ 0
x 2 - 10 x + 25 ≠ 0 ⇔ x - 5 2 ≠ 0 ⇔ x ≠ 5
Vậy điều kiện để biểu thức xác định là x ≠ 0 và x ≠ 5
CM
27 tháng 2 2018
a) Ta có 3 x − 1 10 x 2 + 2 x . 25 x 2 + 10 x + 1 1 − 9 x 2 = − 5 x + 1 2 x ( 3 x + 1 )
b) Kết quả = p . ( p − 3 ) 7
CM
13 tháng 12 2017
Biểu thức x 2 - 25 x 2 + 10 x + 25 x - 5 xác định khi x 2 + 10 x + 25 ≠ 0 và x - 5 ≠ 0
x 2 + 10 x + 25 ≠ 0 ⇔ x + 5 2 ≠ 0 ⇔ x ≠ - 5
x – 5 ≠ 0 ⇔ x ≠ 5
Vậy điều kiện để biểu thức xác định là x ≠ 5 và x ≠ - 5.
TH
1
H9
HT.Phong (9A5)
CTVHS
24 tháng 10 2023
a) \(A=4x^2-4x+23\)
\(A=4x^2-4x+1+22\)
\(A=\left(2x-1\right)^2+22\)
Mà: \(\left(2x-1\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(2x-1\right)^2+22\ge22\forall x\)
Dấu "=" xảy ra:
\(2x-1=0\)
\(\Rightarrow2x=1\)
\(\Rightarrow x=\dfrac{1}{2}\)
Vậy: \(A_{min}=22\Leftrightarrow x=\dfrac{1}{2}\)
b) \(B=25x^2+y^2+10x-4y+2\)
\(B=25x^2+10x+1+y^2-4y+4-3\)
\(B=\left(5x+1\right)^2+\left(y-2\right)^2-3\)
Mà: \(\left\{{}\begin{matrix}\left(5x+1\right)^2\ge0\forall x\\\left(y-2\right)^2\ge0\forall y\end{matrix}\right.\)
\(\Rightarrow B=\left(5x+1\right)^2+\left(y-2\right)^2-3\ge-3\forall x,y\)
Dấu "=" xảy ra:
\(\left\{{}\begin{matrix}5x+1=0\\y-2=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}5x=-1\\y=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{5}\\y=2\end{matrix}\right.\)
Vậy: \(B_{min}=-3\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{5}\\y=2\end{matrix}\right.\)
H
14 tháng 6 2023
`1,(4x^3+3x^3):x^3+(15x^2+6x):(-3x)=0`
`<=> 4 + 3 + (-5x) + (-2)=0`
`<=> -5x+5=0`
`<=>-5x=-5`
`<=>x=1`
`2,(25x^2-10x):5x +3(x-2)=4`
`<=> 5x - 2 + 3x-6=4`
`<=> 8x -8=4`
`<=> 8x=12`
`<=>x=12/8`
`<=>x=3/2`
`3,(3x+1)^2-(2x+1/2)^2=0`
`<=> [(3x+1)-(2x+1/2)][(3x+1)+(2x+1/2)]=0`
`<=>( 3x+1-2x-1/2)(3x+1+2x+1/2)=0`
`<=>( x+1/2) (5x+3/2)=0`
`@ TH1`
`x+1/2=0`
`<=>x=0-1/2`
`<=>x=-1/2`
` @TH2`
`5x+3/2=0`
`<=> 5x=-3/2`
`<=>x=-3/2 : 5`
`<=>x=-15/2`
`4, x^2+8x+16=0`
`<=>(x+4)^2=0`
`<=>x+4=0`
`<=>x=-4`
`5, 25-10x+x^2=0`
`<=> (5-x)^2=0`
`<=>5-x=0`
`<=>x=5`