Cho hình bình hành ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD a) Xác định dạng của các tứ giác AEFD, DEBF. b) Gọi I là giao điểm của AF và DE, K là giao điểm của BF và CE. Xác định dạng của các tứ giác DIKF, IEKF. c) Tìm điều kiện của hình bình hành ABCD để IEKF là hình vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 6:
a: Xét ΔABC có BD/BA=BM/BC
nên MD//AC
=>ME vuông góc với AB
=>E đối xứng M qua AB
b: Xét tứ giác AEBM có
D là trung điểm chung của AB và EM
MA=MB
Do đó; AEBM là hình thoi
Xét tứ giac AEMC có
AE//MC
AE=MC
Do đó: AEMC là hình bình hành
c: BM=BC/2=2cm
=>CAEBM=2*4=8cm

b tham khảo nha
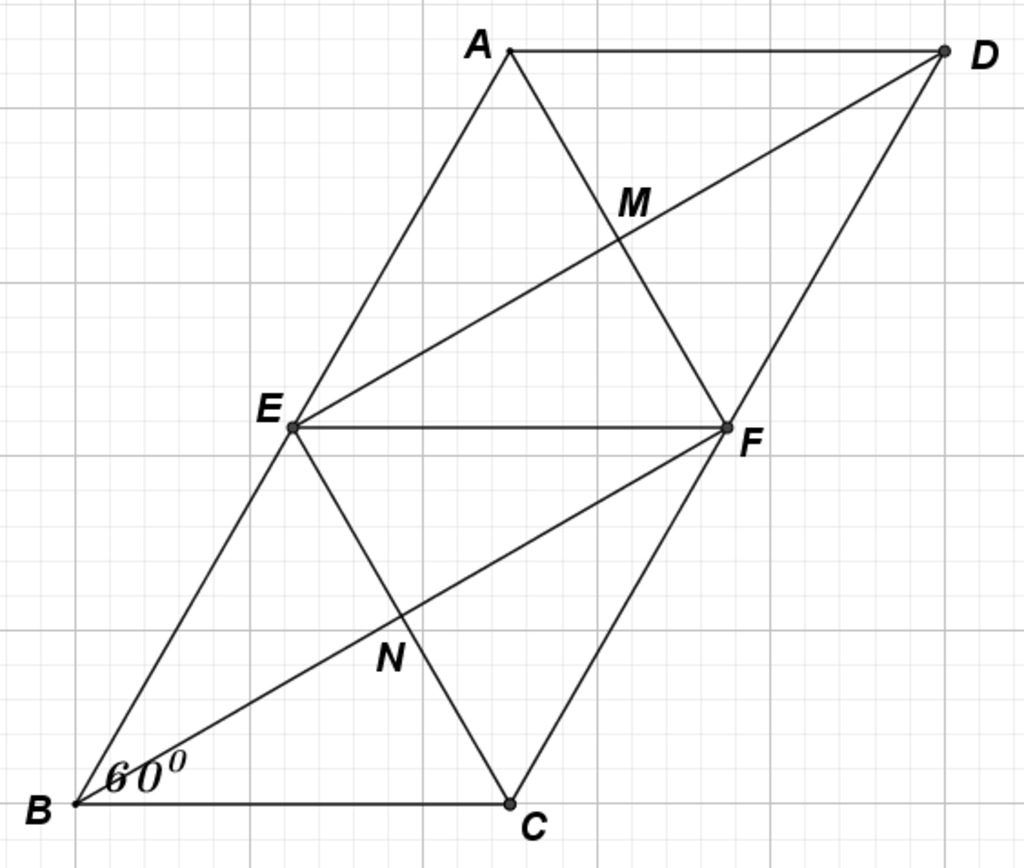
a) Do ABCD là hình bình hành nên AB= CD và AB//CD
Và E và F là trung điểm của AB và CD => AE=BE=CF=DF và BE//DF
Xét tứ giác DEBF có : BE//DF và BE=DF=> DEBF là hình bình hành
b)
Xét AEDF có AE//DF và AE=DF=> AEDF là hình bình hành
Lại có: CD= 2BC= 2 AD nên AD= AE (=1/2 CD)
=> hình bình hành AEDF là hình thoi
c)ta cm được AECF là hình bình hành và M, N là trung điểm của AF và CE
=> MF= EN và MF//EN=> EMFN là hình bình hành
Lại có AEDF là hình thoi nên AN⊥DE tại M
=> góc EMF vuông=> hình bình hành EMFN là hình chữ nhật
d) Chứng minh được
SAFB=12SABCDSBEC=14SABCDˆB=600⇒ΔBECdeucanh=AB2=2(cm)⇒SBEC=√3(cm2)⇒SAFB

a) bạn tự vẽ hình nhé!
Có : \(AE=BE=\frac{1}{2}AB\) (đề cho)
\(DF=CF=\frac{1}{2}DC\) (đề cho)
mà \(AB=CD\)
\(\Rightarrow\) \(AE=BE=DF=CF\)
Xét tứ giác AEFD có:
\(AE=DF\) (cmt) và AE//DF( AB//CD)
\(\Rightarrow\) Tứ giác AEFD là hình bình hành
Xét tứ giác AECF có :
AE = CF ( cmt) và AE//CF ( AB//CD)
\(\Rightarrow\) Tứ giác AECF là hình bình hành
M là giao điểm của AF và DE
\(\Rightarrow\) AM = FM=\(\frac{1}{2}AF\) ( tính chất đ/chéo hbhành) (1)
N là giao điểm của BF và CE
\(\Rightarrow\) EN = CN=\(\frac{1}{2}CE\) ( tính chất đ/chéo hbhành) (2)
Có AF = AM + FM
CE = EN + CN
mà AE = CE ( AECF là hbh)
Từ (1) và (2) suy ra MF= EN và MF//EN ( AF//CE )
\(\Rightarrow\) EMFN là hình bình hành (3)
Có AE = AD ( cùng bằng 2AB ) và AEFD là hình bình hành nên AEFD là hình thoi
\(\Rightarrow\) AF \(\perp\) DE tại M hay góc EMF = 90 độ (4)
Từ (3) và (4) suy ra : EMFN là hcn

Cho hình bình hành ABCD có AB = 2AD. Gọi E là trung điểm của AB,F trung điểm của CD, I là giao điểm của AF và DE, K là giao điểm của BF và CE
a) Tứ giác AECF là hình gì ? Vì sao ?
b) Tứ giác AEFD là hình gì ? Vì sao ?

a) Tứ giác AEFD là hình thoi, tứ giác AECF là hình bình hành (tự chứng minh).
b) Tứ giác AECF là hình bình hành nên EN // FM. Tứ giác AECF là hình bình hành nên EM // FN. AEFD là hình thoi nên AF \(\perp\) DE.
Hình bình hành EMFN có \(\widehat{M}=90^o\) nên là hình chữ nhật.
c) Hình chữ nhật EMFN là hình vuông
\(\Leftrightarrow\) ME = MF \(\Leftrightarrow\) DE = AF (vì DE = 2ME, AF = 2MF)
\(\Leftrightarrow\) Hình thoi AEFD có hai đường chéo bằng nhau
\(\Leftrightarrow\) AEFD là hình vuông \(\Leftrightarrow\) \(\widehat{A}=90^o\).
\(\Leftrightarrow\) Hình bình hành ABCD là hình chữ nhật.
Như vậy, hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật.

Bài 8:
a: Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
mà AE=AD
nên AEFD là hình thoi

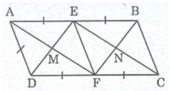
Tứ giác AEFD là hình thoi
⇒ AF ⊥ ED ⇒ ∠ (EMF) = 90 0
AF // CE (vì tứ giác AECF là hình bình hành)
Suy ra: CE ⊥ ED ⇒ ∠ (MEN) = 90 0
Xét tứ giác EBFD, ta có: EB = FD (vì cùng bằng AE)
EB // FD (vì AB // CD)
Tứ giác EBFD là hình bình hành (vì có một cặp cạnh đổi song song và bằng nhau) ⇒ DE // BF
Suy ra: BF ⊥ AF ⇒ ∠ (MFN) = 90 0
Vậy tứ giác EMFN là hình chữ nhật.

a: E là trung điểm của AB
=>\(AE=EB=\dfrac{AB}{2}\left(1\right)\)
F là trung điểm của CD
=>\(FC=FD=\dfrac{CD}{2}\left(2\right)\)
ABCD là hình bình hành
=>AB=CD(3)
Từ (1),(2),(3) suy ra AE=EB=CF=FD=AB/2
mà AD=BC=AB/2
nên AE=EB=CF=FD=AD=BC
Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
Hình bình hành AEFD có AE=AD
nên AEFD là hình thoi
Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: Xét tứ giác BEFC có
BE//FC
BE=FC
Do đó: BEFC là hình bình hành
Hình bình hành BEFC có BE=BC
nên BEFC là hình thoi
=>EC vuông góc BF tại trung điểm của mỗi đường
=>EC vuông góc BF tại K và K là trung điểm chung của EC và BF
AEFD là hình thoi
=>AF vuông góc ED tại trung điểm của mỗi đường
=>AF vuông góc ED tại I và I là trung điểm chung của AF và ED
Xét ΔEDC có
I,K lần lượt là trung điểm của ED,EC
=>IK là đường trung bình của ΔEDC
=>IK//DC và IK=DC/2
IK=DC/2
DF=DC/2
Do đó: IK=DF
IK//DC
\(F\in DC\)
Do đó: IK//DF
Xét tứ giác DIKF có
IK//DF
IK=DF
Do đó: DIKF là hình bình hành
Xét ΔEDC có
EF là đường trung tuyến
\(EF=\dfrac{DC}{2}\)
Do đó: ΔEDC vuông tại E
Xét tứ giác EIFK có
\(\widehat{EIF}=\widehat{EKF}=\widehat{IEK}=90^0\)
=>EIFK là hình chữ nhật
c: Hình chữ nhật EIFK là hình vuông khi EI=FI
=>ED=AF
Hình thoi AEFD có ED=AF
nên AEFD là hình vuông
=>\(\widehat{BAD}=90^0\)