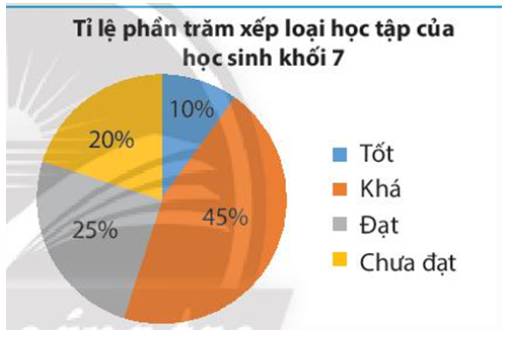
Kết quả xếp loại học tập cuối học kì 1 của học sinh khối 7 được cho ở biểu đồ bên. Gặp ngẫu nhiên một học sinh khối 7
a) Xác suất học sinh đó được xếp loại học lực nào là cao nhất?
b) Xác suất học sinh đó được xếp loại học lực nào là thấp nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số học sinh xếp loại tốt là
\(120\times\dfrac{4}{15}=32\) ( học sinh )
Số học sinh xếp loại khá là
\(32\div80\%=40\) ( học sinh )
a) Số học sinh xếp loại đạt là
\(120-32-40=48\) ( học sinh )
b) Tỉ số phần trăm số học sinh xếp loại khá so với học sinh cả khối là
\(\dfrac{40\times100}{120}\%=33,333...\%\approx33,33\%\)

Chọn D
Ω “Xếp 10 học sinh thành một hàng ngang” => n( Ω ) = 10!
A “Không có học sinh khối 11 nào xếp giữa hai học sinh khối 10”.
Trường hợp I (2 học sinh khối 10 đứng cạnh nhau):
Bước 1: Buộc 2 học sinh khối 10 thành một phần tử X và đổi chỗ 2 học sinh đó có 2! cách.
Bước 2: Xếp phần tử X và 8 học sinh còn lại thành một hàng ngang có 9! cách.
Vậy, có 9!.2! cách.
Trường hợp II (giữa 2 học sinh khối 10 có 1 học sinh khối 12):
Bước 1: Chọn 1 học sinh khối 12 trong 3 học sinh có C 3 1 cách.
Bước 2: Buộc 2 học sinh khối 10 và học sinh khối 12 đã chọn thành một phần tử X rồi đổi chỗ 2 học sinh khối 10 có 2! cách.
Bước 3: Xếp phần tử X và 7 học sinh còn lại thành một hàng ngang có 8! cách.
Vậy, có C 3 1 .2!.8! cách.
Trường hợp III (giữa 2 học sinh khối 10 có 2 học sinh khối 12):
Bước 1: Chọn 2 học sinh khối 12 trong 3 học sinh có C 3 2 cách.
Bước 2: Buộc 2 học sinh khối 10 và 2 học sinh khối 12 đã chọn thành một phần tử X rồi đổi chỗ 2 học sinh khối 10, đổi chỗ 2 học sinh khối 12 có 2!.2! cách.
Bước 3: Xếp phần tử X và 6 học sinh còn lại thành một hàng ngang có 7! cách.
Vậy, có C 3 2 .2!.2!.7!cách.
Trường hợp IV (giữa 2 học sinh khối 10 có 3 học sinh khối 12):
Bước 1: Buộc 2 học sinh khối 10 và 3 học sinh khối 12 đã chọn thành một phần tử X rồi đổi chỗ 2 học sinh khối 10, đổi chỗ 3 học sinh khối 12 có 2!.3! cách.
Bước 2: Xếp phần tử X và 5 học sinh còn lại thành một hàng ngang có 6! cách.
Vậy, có 2!.3!.6! cách.
Theo quy tắc cộng, ta được ![]()
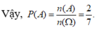

Bài giải
Số HS trung bình chiếm:
1 -( \(\frac{1}{5}+\frac{1}{3}\))= \(\frac{7}{15}\)(tổng HS lớp 5)
a)HS khối 5 của trường đó là:
70 : 7 x 15 = 150(HS)
b)HS giỏi là:
150 x \(\frac{1}{5}\)= 30 (HS)
HS khá là:
150 x \(\frac{1}{3}\)= 50(HS)
Đáp số: a) 150 HS
b) khá 50 HS
giỏi 30 HS
Bài giải
Số học sinh trung bình chiếm số phần tổng số học sinh lớp 5 là:
\(1-\left(\frac{1}{5}+\frac{1}{3}\right)=\frac{7}{15}\)(tổng số học sinh lớp 5)
a) Số học sinh Khối 5 của trường là:
\(70\div7\times15=150\)(học sinh)
b) Số học sinh giỏi là:
\(150\times\frac{1}{5}=30\)(học sinh)
Số học sinh khá là:
\(150\times\frac{1}{3}=50\)(học sinh)
Đáp số: a) 150 học sinh
b) 30 học sinh
50 học sinh

Tỉ lệ phần trăm học sinh xếp loại:
+ Tốt: \(\frac{{36}}{{360}}.100\% = 10\% \)
+ Khá: \(\frac{{162}}{{360}}.100\% = 45\% \)
+ Đạt: \(\frac{{90}}{{360}}.100\% = 25\% \)
+ Chưa đạt: \(\frac{{72}}{{360}}.100\% = 20\% \)
Kết quả này hoàn toàn trùng khớp với giá trị tương ứng trong biểu đồ trên.

Số hs Khá là.
180.35%=63(em)
Số hs Trung Bình là.
63:7/9=81(em)
Số hs Yếu là.
180.1/15=12(em)
Số hs giỏi là
180-(63+81+12+3)=21(em)
Vậy :hs Khá 63 em
hs T B 81 em *Dấu chấm là dấu nhân nhé!
hs yếu 12 em
hs Giỏi 21 em

Tổng số phần xếp loại giỏi và loại khá của học sinh khối 5 là: 1/5+1/3=8/15
70 em xếp loại trung bình ứng với số phần là: 1-8/15=7/15(số học sinh khối 5)
a) Số học sinh khối 5 là: 70 : 7x15 = 150 (học sinh)
b) Số học sinh xếp loại giỏi là:
150x1/5=30(học sinh)
Số học sinh xếp loại khá là:
150 x1/3=50(học sinh)
Tỉ số phần trăm của số học sinh xếp loại giỏi và số học sinh của toàn khối là:
30 : 150=20%(số học sinh của toàn khối)
Đáp số :a)150 học sinh
b)20% số học sinh của toàn khối

a ) Số học sinh khối 5 : 150 học sinh
b ) Giỏi :30 học sinh
Khá : 50 học sinh
k mình đi ! Mình giải cho
a) Theo biểu đồ tỉ lệ xếp loại học lực học sinh khối 7 tỉ lệ học sinh khá chiếm nhiều nhất nên nếu gặp ngẫu nhiên thì tỉ lệ gặp học sinh xếp loại khá là cao nhất.
b) Vì tỉ lệ học sinh xếp loại tốt là thấp nhất nên nếu gặp ngẫu nhiên thì tỉ lệ gặp học sinh sếp loại tốt là thấp nhất.