Cho hai máy tính xách tay (laptop) có kích thước màn hình (tính theo đơn vị mm) lần lượt là 227,6 × 324 và 170,7 × 243. Tính tỉ số giữa chiều rộng và chiều dài của mỗi màn hình.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 11 2023
Gọi chiều dài, chiều rộng lần lượt là a(inch) và b(inch)
Chiều dài, chiều rộng lần lượt tỉ lệ với 16 và 9 nên a/16=b/9
Đặt \(\dfrac{a}{16}=\dfrac{b}{9}=k\)
=>a=16k; b=9k
Kích thước đường chéo là 55inch nên \(a^2+b^2=55^2\)
=>\(\left(16k\right)^2+\left(9k\right)^2=55^2\)
=>\(256k^2+81k^2=55^2\)
=>\(k^2=\dfrac{3025}{337}\)
=>\(k=\dfrac{55}{\sqrt{337}}\)
=>\(a=16\cdot\dfrac{55}{\sqrt{337}}=\dfrac{880}{\sqrt{337}};b=9\cdot\dfrac{55}{\sqrt{337}}=\dfrac{495}{\sqrt{337}}\)
=>\(a=\dfrac{880}{\sqrt{337}}inch\simeq121,76\left(cm\right)\)
\(b=\dfrac{495}{\sqrt{337}}inch=68,49\left(cm\right)\)
1 tháng 11 2023
24inch=60,96(cm)
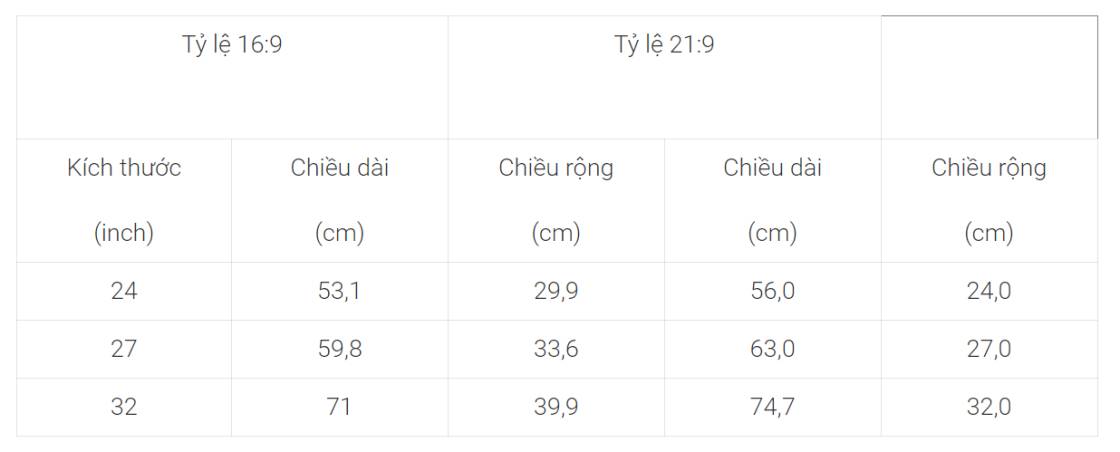
Gọi chiều dài, chiều rộng của màn hình lần lượt là a(cm),b(cm)(ĐK: a>0 và b>0)
Chiều dài, chiều rộng lần lượt tỉ lệ với 16 và 9
nên ta có: \(\dfrac{a}{16}=\dfrac{b}{9}\)
Đặt \(\dfrac{a}{16}=\dfrac{b}{9}=k\)
=>a=16k; b=9k
Kích thước của máy tính là 60,96cm nên ta có:
\(a^2+b^2=60,96^2\)
=>\(256k^2+81k^2=60,96^2\)
=>\(k^2\simeq11,03\)
=>\(k\simeq3,32\)
=>\(\left\{{}\begin{matrix}a\simeq53,12\left(cm\right)\\b\simeq29,88\left(cm\right)\end{matrix}\right.\)
21 tháng 7 2023
Độ dài đường chéo là:
\(\sqrt{72^2+120^2}=24\sqrt{34}\left(cm\right)\simeq55,1\left(inch\right)\)
H9
HT.Phong (9A5)
CTVHS
14 tháng 7 2023
Ta có góc của màng hình tivi là góc vuông nên đường cheo của tivi là:
\(\sqrt{72^2+120^2}=24\sqrt{34}\left(cm\right)\)
Đổi: \(24\sqrt{34}\left(cm\right)\approx55\left(inch\right)\)
Vậy: ...
KV
16 tháng 11 2023
Ta có:
23² + 40² = 2129
Độ dài đường chéo màn hình:
√2129 : 2,54 ≈ 18,2 (inch)
G
14 tháng 8 2023
Cách 1:
\(\dfrac{BC}{sin\widehat{A}}=\dfrac{AB}{sin\widehat{C}}=\dfrac{AC}{sin\widehat{B}}\)
Ta có \(\widehat{C}=\widehat{B}\) ( tam giác ABC cân tại A )
\(\widehat{B}+\widehat{C}=180^0-\widehat{A}\) \(\Leftrightarrow2\widehat{B}=180^0-\widehat{A}\Leftrightarrow\widehat{B}=90^0-\dfrac{\widehat{A}}{2}\)
\(\Rightarrow sin\widehat{B}=sin\left(90^0-\dfrac{\widehat{A}}{2}\right)=cos\left(\dfrac{\widehat{A}}{2}\right)\)
\(\Rightarrow\dfrac{BC}{sin\widehat{A}}=\dfrac{AC}{cos\left(\dfrac{\widehat{A}}{2}\right)}\) \(\Leftrightarrow\sqrt{3}.cos\left(\dfrac{\widehat{A}}{2}\right)=2.sin\left(\dfrac{\widehat{A}}{2}\right).cos\left(\dfrac{\widehat{A}}{2}\right)\)
( tam giác ABC có \(\widehat{A}\ne180^0\Rightarrow\dfrac{\widehat{A}}{2}\ne90^0\Rightarrow cos\left(\dfrac{\widehat{A}}{2}\right)\ne0\) )
\(\Rightarrow\sqrt{3}=2sin\left(\dfrac{\widehat{A}}{2}\right)\) \(\Leftrightarrow\dfrac{\widehat{A}}{2}=60^0\Leftrightarrow\widehat{A}=120^0\)
Vậy độ mở của màn hình máy tính là \(120^0\)
Cách 2: Do AB=AC nên tam giác ABC cân tại A
Kẻ \(AH\perp BC\) tại H
Tam giác ABC cân tại A có AH vừa là đường cao, vừa là đường phân giác, vừa là đường trung tuyến
\(\Rightarrow\)H là trung điểm của BC \(\Rightarrow BH=\dfrac{BC}{2}=15\sqrt{3}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông có:
\(sin\widehat{BAH}=\dfrac{BH}{AB}=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{BAH}=60^0\)
\(\Rightarrow\widehat{BAC}=2\widehat{BAH}=120^0\)
Vậy độ mở của màn hình máy tính là \(120^0\)
H9
HT.Phong (9A5)
CTVHS
27 tháng 7 2023
Ta có hai cạnh của tivi và đường chéo tạo thành một tam giác vuông nên:
Độ dài đường chéo chính là cạnh huyền:
Áp dụng định lý Py-ta-go ta có được độ dài đường chéo tivi là:
\(\sqrt{72^2+120^2}=24\sqrt{34}\left(cm\right)=24\sqrt{34}:2,54=55,1\left(inch\right)\)
27 tháng 7 2023
Độ dài đường chéo là:
\(\sqrt{72^2+120^2}=24\sqrt{34}\left(cm\right)\simeq55,10\left(inch\right)\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
+) Gọi x là chiều dài của màn hình ti vi
y là chiều rộng của màn hình ti vi
+) Ta có hệ phương trình:
\( \Rightarrow \left\{ \begin{array}{l}{x^2} + {y^2} = {32^2}\\\frac{x}{y} = \frac{{16}}{9}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \approx 27,890417\\y \approx 15,688359\end{array} \right.\) . Vậy chiều dài của ti vi là: 27,890417 (in)
+) Nếu lấy giá trị gần đúng của x là 27,89 thì: \(27,89 < x < 27,895\)
Suy ra: \(\left| {x - 27,89} \right| < 27,895 - 27,89 = 0,005\)
Vậy độ chính xác của số gần đúng là 0,005
+) Sai số tương đối của số gần đúng là: \(\delta = \frac{{0,005}}{{\left| {27,89} \right|}} = 0,018\% \)
Tỉ số giữa chiều rộng và chiều dài của màn hình thứ nhất: \(\dfrac{227,6}{324}\)
Tỉ số giữa chiều rộng và chiều dài của màn hình thứ hai: \(\dfrac{170,7}{243}\)
#kễnh