S = 2. 10 + 2. 12 + 2. 14 + … + 2. 20 cứu mấy ní tui mới lên lớp 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TL
0
PT
0
PV
12
NT
Nguyễn Tuấn Tú
CTVHS
26 tháng 10 2023
\(\dfrac{2}{3}+\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{24}+\dfrac{2}{48}+\dfrac{2}{96}+\dfrac{2}{192}\\ =\dfrac{128}{192}+\dfrac{64}{192}+\dfrac{32}{192}+\dfrac{16}{192}+\dfrac{8}{192}+\dfrac{4}{192}+\dfrac{2}{192}\\ =\dfrac{128+64+32+16+8+4+2}{192}\\ =\dfrac{254}{192}=\dfrac{127}{96}\)
19 tháng 9 2017
a.=47-[45.16-25.12]:14]
=47-420:14
=47-30
=17
b.=50-[12:2+34]
=50-40
=10
c.=100-60:10
=100-6
=94
d.50-[(50-40);2+3]
=50-(10:2+3)
=50-8
=42
AH
Akai Haruma
Giáo viên
2 tháng 1
Bài 5:
Với $x,y$ là số nguyên thì $x+1, xy-1$ cũng là số nguyên. Mà tích của chúng bằng 3 nên ta có các TH sau:
TH1: $x+1=1, xy-1=3\Rightarrow x=0; xy=3$ (vô lý - loại)
TH2: $x+1=-1, xy-1=-3\Rightarrow x=-2; xy=-2\Rightarrow y=1$ (thỏa mãn)
TH3: $x+1=3; xy-1=1\Rightarrow x=2; xy=2\Rightarrow y=1$ (thỏa mãn)
TH4: $x+1=-3; xy-1=-1\Rightarrow x=-4; xy=0$ (vô lý -loại)
Vậy......
AH
Akai Haruma
Giáo viên
2 tháng 1
Bài 6:
$\frac{a}{7}-\frac{1}{2}=\frac{1}{b+3}$
$\Rightarrow \frac{2a-7}{14}=\frac{1}{b+3}$
$\Rightarrow (2a-7)(b+3)=14$
Với $a,b$ nguyên thì $2a-7, b+3$ cũng là số nguyên. Mà $(2a-7)(b+3)=14$ và $2a-7$ là số nguyên lẻ nên ta các TH sau:
TH1: $2a-7=1; b+3=14\Rightarrow a=4; b=11$ (thỏa mãn)
TH2: $2a-7=-1; b+3=-14\Rightarrow a=3; b=-17$ (thỏa mãn)
TH3: $2a-7=7; b+3=2\Rightarrow a=7; b=-1$ (thỏa mãn)
TH4: $2a-7=-7; b+3=-2\Rightarrow a=0; b=-5$ (thỏa mãn)
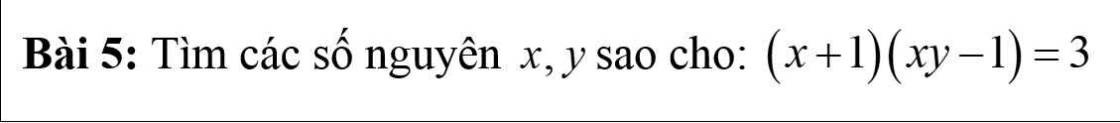
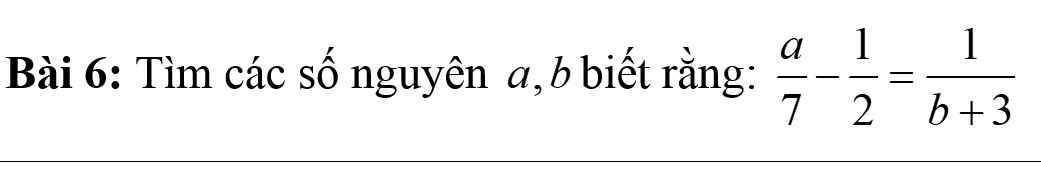
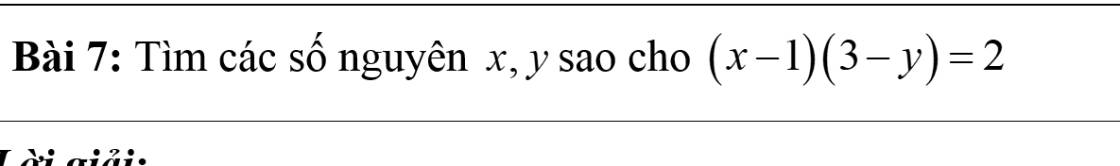
`# \text {04th5.}`
`S = 2.10 + 2.12 + 2.14 + ... + 2. 20`
`= 2.2.5 + 2.2.6 + 2.2.7 + ... + 2.2.10`
`= 2^2 . 5 + 2^2 . 6 + 2^2 . 7 + ... + 2^2 . 10`
`= 2^2 . (5 + 6 + 7 + 8 + 9 + 10)`
`= 2^2 . 45`
`= 4.45 = 180`
Vậy, `S = 180.`
S=2.10+2.12+2.14+...+2.20
S=22.5+22.6+22.7+...+22.10
S=4.(5+6+7+8+9+10)
S=4.45=180