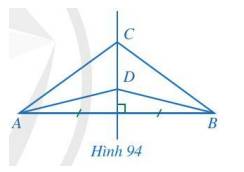
Trong Hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh \(\widehat {CAD} = \widehat {CBD}\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì d là đường trug trực của AB mà C,D thuộc d nên: AC=BC =>tam giác ACB cân tại C=> Góc CAB= góc CBA (1)
AD=BD=>tam giácABD cân tại D=> Góc DAB= góc DBA (2)
TỪ (1) và

a) Ta có: đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên \(a \bot AB;a \bot CD\).
Suy ra: AB // CD.
b) Đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên MN là đường trung trực của đoạn thẳng AB và CD. Suy ra: MD = MC.
Xét tam giác vuông MNC và tam giác vuông MND có: ND = NC; MD = MC.
Vậy \(\Delta MNC = \Delta MND\)(cạnh huyền – cạnh góc vuông).
c) \(\Delta MNC = \Delta MND\)nên \(\widehat {CMN} = \widehat {DMN}\).
Mà \(\widehat {AMN} = \widehat {BMN} = 90^\circ \Rightarrow \widehat {AMN} - \widehat {DMN} = \widehat {BMN} - \widehat {CMN}\).
Vậy \(\widehat {AMD} = \widehat {BMC}\).
d) Xét hai tam giác AMD và BMC có:
MA = MB;
\(\widehat {AMD} = \widehat {BMC}\);
MD = MC.
Vậy \(\Delta MAD = \Delta MBC\)(c.g.c). Suy ra: \(AD = BC,\widehat A = \widehat B\) (cặp cạnh và góc tương ứng).
e) \(\Delta MAD = \Delta MBC\) nên \(\widehat {ADM} = \widehat {BCM}\) (2 góc tương ứng).
\(\Delta MNC = \Delta MND\) nên \(\widehat {MCN} = \widehat {MDN}\) (2 góc tương ứng).
Vậy \(\widehat {ADM} + \widehat {MDN} = \widehat {BCM} + \widehat {MCN}\) hay \(\widehat {ADC} = \widehat {BCD}\).

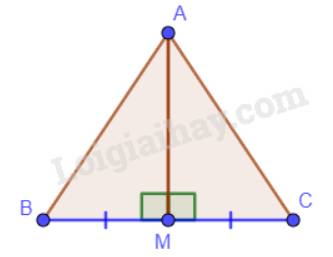
M là trung điểm của BC nên B, M, C thằng hàng → \(\widehat {BMC} = 180^\circ \). Mà \(\widehat {AMB} = \widehat {AMC}\)nên \(\widehat {AMB} = \widehat {AMC} = 180^\circ :2 = 90^\circ \)→ \(AM \bot BC\).
Vậy AM đi qua trung điểm M của đoạn thẳng BC và AM vuông góc với BC. Hay AM là đường trung trực của đoạn thẳng BC.
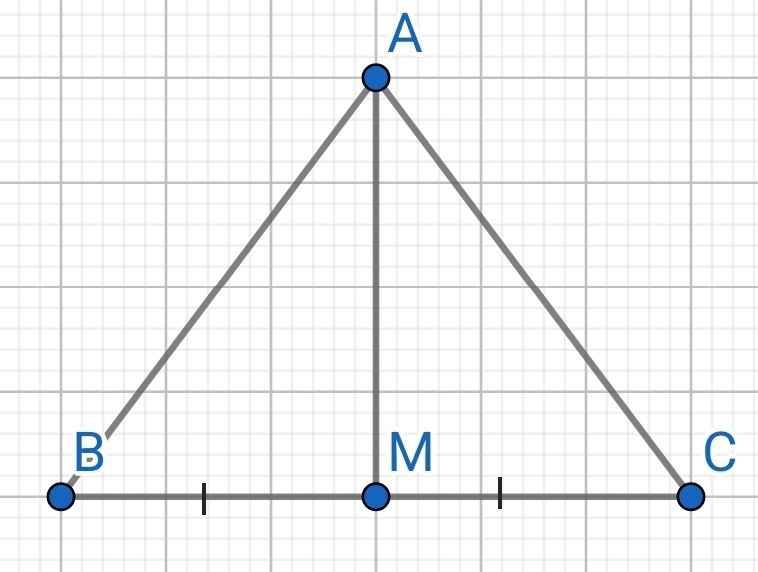 Ta có:
Ta có:
∠AMB + ∠AMC = 180⁰ (kề bù)
Mà ∠AMB = ∠AMC (gt)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
Mà M là trung điểm của BC
⇒ AM là đường trung trực của BC

Cho hình thang cân ABCD (BC//AD), hai đường chéo AC, BD cắt nhau tại điểm O sao cho \widehat{BOC} = 60 độ. Gọi M,N,P,Q lần lượt là trung điểm của các đoạn thẳng BC,OA,AB,CD.a) Chứng minh tứ giác DMNC nội tiếp đượcb) Chứng minh tam giác MNQ là tam giác đềuc) So sánh các góc \widehat{MQP}, \widehat{QND}, \widehat{NMC} d) Chứng minh trực tâm của tam giác MNQ thẳng hàng với O, I

a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)
Ta có: đường thẳng CD là đường trung trực của đoạn thẳng AB nên CA=CB và DA=DB.
Ta có tam giác ABC cân tại C, tam giác DAB cân tại D
Suy ra \(\widehat {CAB} = \widehat {CBA};\widehat {DAB} = \widehat {DBA}\).
Vậy \(\widehat {CAB} - \widehat {DAB} = \widehat {CBA} - \widehat {DBA}\) suy ra: \(\widehat {CAD} = \widehat {CBD}\).