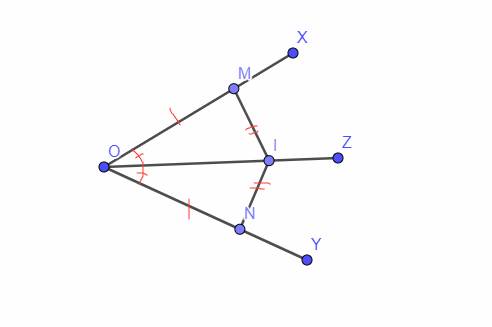
Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thỏa mãn OM = ON, điểm P khác O và thuộc Oz. Chứng minh MP = NP.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a,` Xét Tam giác `OIM` và Tam giác `OIN` có:
`OM = ON (g``t)`
\(\widehat{MOI}=\widehat{NOI}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OI` chung
`=>` Tam giác `OIM =` Tam giác `OIN (c-g-c)`
`b,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`->` \(\widehat{OIM}=\widehat{OIN}\) `( 2` góc tương ứng `)`
`c,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`-> IM = IN (2` cạnh tương ứng `)`
`\color{blue}\text {#DuyNam}`

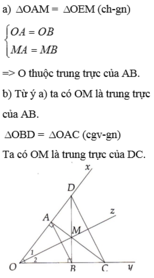
a)
Xét \(\Delta\)OAC và \(\Delta\)OBC có:
^CAO = ^CBO ( = 90\(^o\))
OC chung
^AOC = ^BOC ( OC là phân giác ^xOy)
=> \(\Delta\)OAC = \(\Delta\)OBC ( cạnh huyền - góc nhọn) => OA = OB
b) \(\Delta\)OAC = \(\Delta\)OBC => CA = CB ; ^BCO = ^ACO
Xét \(\Delta\)IAC và \(\Delta\)I BC có: CA = CB ; ^BCI = ^ACI ( vì ^BCO = ^ACO ) ; CI chung
=> \(\Delta\)IAC = \(\Delta\)IBC ( c.g.c) (1)
=> IA = IB => I là trung điểm AB (2)
c) từ (1) => ^AIC = ^BIC mà ^AIC + ^BIC = 180\(^o\)
=> ^AIC = ^BIC = \(90^o\)
=> CI vuông góc AB
=> CO vuông goác AB tại I (3)
Từ (2) ; ( 3) => CO là đường trung trực của đoạn thẳng AD.

Xét tam giác MOP và tam giác NOP có: OM = ON, OP chung, \(\widehat {MOP} = \widehat {NOP}\)(vì Oz là tia phân giác).
Vậy \(\Delta MOP = \Delta NOP\)(c.g.c)
\(\Rightarrow MP = NP\) ( 2 cạnh tương ứng)