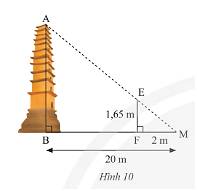
Trong Hình 10, biết \(MB = 20m,MF = 2m,EF = 1,65m\). Tính chiều cao \(AB\) của ngọn tháp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
24 tháng 8 2023
Chiều của ngọn tháp là:
\(\dfrac{99}{4}:2=\dfrac{99}{8}\left(m\right)\)
Đáp số: \(\dfrac{99}{8}m\)
24 tháng 8 2023
Chiều cao của ngọn tháp là:
\(\dfrac{99}{4}:2=\dfrac{99}{8}\left(m\right)\)
C
8 tháng 1 2024
a) Đổi \(20m^2=2000dm^2\)
Chiều cao của hình thang đó là:
\(2000\times2:\left(55+45\right)=40\left(m\right)\)
Đáp số: \(40m\)
b) Tổng độ dài 2 đáy của hình thang là:
\(7\times2\div2=7\left(m\right)\)
Trung bình cộng của 2 đáy là:
\(7:2=3,5\left(m\right)\)
Đáp số: \(3,5m\)
29 tháng 12 2014
bài giải
a) chiều cao hinh thang là;
(45+55):2=50(dm)
b) trung bình cộng hai đáy là:
7:2=3,5(m)
đáp số:a)50m
b)3,5m
Xét \(\Delta MEF\) và \(\Delta MAB\) có:
\(\widehat M\) chung
\(\widehat {MFE} = \widehat {MBA} = 90^\circ \)
Do đó, \(\Delta MEF\backsim\Delta MAB\) (g.g)
Vì nên \(\frac{{MF}}{{MB}} = \frac{{FE}}{{AB}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{2}{{20}} = \frac{{1,65}}{{AB}} \Rightarrow AB = \frac{{1,65.20}}{2} = 16,5\)
Vậy tòa tháp cao 16,5m.